Question

Sketch the graphs of the following functions

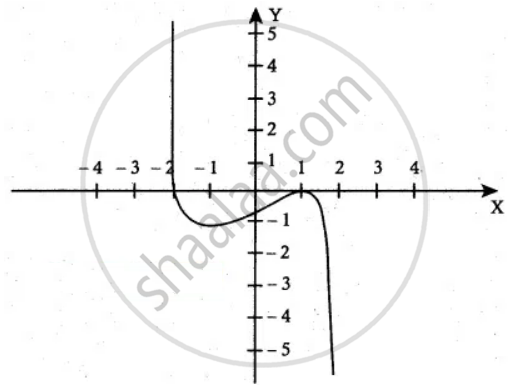
y = `- 1/3 (x^3 - 3x + 2)`

Answer 1

Factorizing we get

y = `- 1/3 (x - 1)^2 (x - 2)` = f(x)

The domain and the range of the given function f(x) are the entire real line.

Putting y = 0

We get x = 1, 1, – 2.

Hence the x-intercepts are (1, 0) and (– 2, 0) and by putting x = 0. 

We get y = `- 2/3`.

Therefore, the y-intercept is `(0, - 2/3)`

f'(x) = f'(x)

= `((3x^2 - 3))/3`

= – (x² – 1)

= 1 – x² 

f'(x) = 0

⇒ 1 – x² = 0

⇒ x = ± 1

The critical points of the curve occur at x = ± 1 .

f”(x) = – 2x

f”(1) = – 2 < 0,

∴ f(x) is maximum at x = 1 and the local maximum is f(1) = 0

f”(– 1) = 2 > 0,

∴ f(x) is minimum at x = – 1 and the local minimum is f(– 1) = `- 4/3`

f”(x) = – 2x < 0 ∀ x > 0

∴ The function is concave downward in the positive real line.

f”(x) = 2x > 0 ∀ x < 0

∴ The function is concave upward in the negative real line.

Since f”(x) = 0 at x = 0 and f”(x) changes its sign when passing through x = 0.

Hence the point of inflection is `(0, - 2/3)`

The curve has no asymptotes.