Advertisements
Advertisements
प्रश्न
Sketch the graphs of the following functions:
y = `xsqrt(4 - x)`
उत्तर
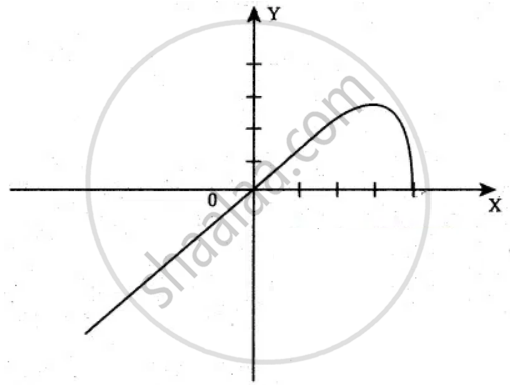
y = `xsqrt(4 - x)` = f(x)
Where x > 4 the curve does not exist and it exists for x ≤ 4
∴ The domain is `(-oo, 4]` and the Range is `(- oo, 16/(3sqrt(3))]`
The curve passes through the origin.
The curve intersects x-axis at (4, 0).
f'(x) = `- x/(2sqrt(4 - x)) + sqrt(4 - x)`
= `(8 - 3x)/(2sqrt(4 - x))`
f'(x) = 0
⇒ 8 – 3x = 0
⇒ x = `8/3`
∴ Critical point of the curve occur at x = `8/3`
f”(x) = `(3x - 16)/(4(4 - x)^(3/2))`
`"f''"(8/3) = - (3sqrt(3))/4 < 0`
∴ f(x) is maximum at x = `8/3` and the total maximum `"f"(8/3) = 16/(3sqrt(3))` and ocal minimum is 0 at x = 4 .......(From the graph)
f”(x) = `(3x - 16)/(4(4 - x)^(3/2))` < 0 ∀ x < 4
∴ The curve is concave downward in the negative real line.
No point of inflection exists.
As `x → oo, y → +- oo` , and hence the curve does not have any asymptotes.
