Advertisements
Advertisements
प्रश्न
समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
उत्तर
PQRS को देखते हुए एक ट्रेपेज़ियम है जिसमें PQ || RS और PQ = 3 RS
⇒ `("PQ")/("RS") = 3/1` ...(i)
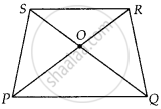
∆POQ और ∆ROS में,
∠SOR = ∠QOP ...[लंबवत विपरीत कोण]
∠SRP = ∠RPQ ...[वैकल्पिक कोण]
∴ ∆POQ ~ ∆ROS ...[AAA समानता मानदंड द्वारा]
इसी तरह के त्रिभुज के क्षेत्र की संपत्ति द्वारा,
`("ar(∆POQ)")/("ar(∆SOR)") = ("PQ")^2/("RS")^2`
= `("PQ"/"RS")^2`
= `(3/1)^2` ...[समीकरण से (i)]
⇒ `("ar(∆POQ)")/("ar(∆SOR)") = 9/1`
इसलिए, आवश्यक अनुपात 9 : 1 है।
APPEARS IN
संबंधित प्रश्न
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
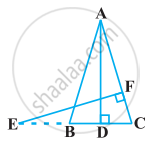
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ∼ ∆ECF है।
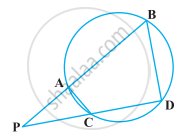
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
क्या यह कहना सत्य है कि यदि दो त्रिभुज में, एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हैं, तो त्रिभुज समरूप होंगे? अपने उत्तर के लिए कारण दीजिए।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
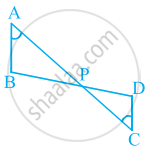
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
यह दिया है कि ΔABC ~ ΔEDF इस प्रकार है कि AB = 5 cm, AC = 7 cm, DF = 15 cm और DE = 12 cm है। इन त्रिभुजों की शेष भुजाओं की लंबाइयाँ ज्ञात कीजिए।
