Advertisements
Advertisements
प्रश्न
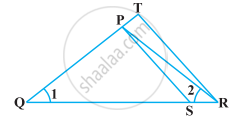
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

उत्तर
प्रश्न के अनुसार,
ΔNSQ ≅ ΔMTR
∠1 = ∠2
चूंकि,
∆NSQ = ∆MTR
तो,
SQ = TR ...(i)
भी,
∠1 = ∠2 ⇒ PT = PS ...(ii) [चूंकि, समान कोणों के विपरीत पक्ष भी समान हैं।]
समीकरण (i) और (ii) से,
`("PS")/("SQ") = ("PT")/("TR")`
⇒ ST || QR
आधारभूत समानुपातिकता प्रमेय के व्युत्क्रम से, यदि एक त्रिभुज की एक भुजा के समांतर अन्य भुजाओं को अलग-अलग बिंदुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाती है, तो अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
∴ ∠1 = PQR
और
∠2 = ∠PRQ
∆PTS और ∆PRQ में,
∠P = ∠P ...[उभयनिष्ठ कोण]
∠1 = ∠PQR ...(सिद्ध)
∠2 = ∠PRQ ...(सिद्ध)
∴ ∆PTS – ∆PRQ ...[AAA समानता मानदंड द्वारा]
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
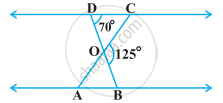
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
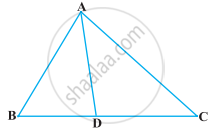
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
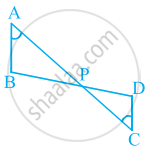
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।