Advertisements
Advertisements
प्रश्न
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
पर्याय
BC . EF = A C. FD
AB . EF = AC . DE
BC . DE = AB . EF
BC . DE = AB . FD
उत्तर
BC . DE = AB . EF
स्पष्टीकरण:
हम जानते हैं कि,
यदि एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती हों, और संगत कोण भी बराबर हों, तो त्रिभुज SSS सममिति द्वारा समरूप होते हैं।
इसलिए, ∆ABC ∼ ∆EDF
समानता संपत्ति का उपयोग करना,
`("AB")/("ED") = ("BC")/("DF") = ("AC")/("EF")`
`("AB")/("ED") = ("BC")/("DF")` लेने पर, हमें प्राप्त होता है।
`("AB")/("ED") = ("BC")/("DF")`
AB . DF = ED . BC
इसलिए, विकल्प (d) BC . DE = AB . FD सत्य है।
`("BC")/("DF") = ("AC")/("EF")` लेने पर, हमें प्राप्त होता है।
`("BC")/("DF") = ("AC")/("EF")`
⇒ BC . EF = AC . DF
इसलिए, विकल्प (a) BC . EF = AC . FD सत्य है।
`("AB")/("ED") = ("AC")/("EF")` लेने पर, हमें प्राप्त होता है।
`("AB")/("ED") = ("AC")/("EF")`
AB . EF = ED . AC
इसलिए, विकल्प (b) AB . EF = AC . DE सत्य है।
APPEARS IN
संबंधित प्रश्न
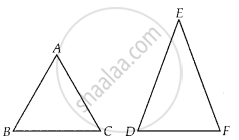
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
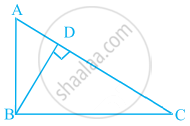
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
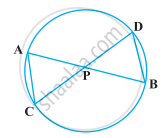
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
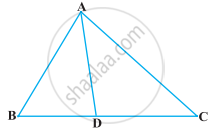
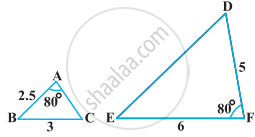
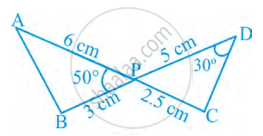
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
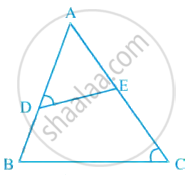
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।