Advertisements
Advertisements
Question
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
Options
BC . EF = A C. FD
AB . EF = AC . DE
BC . DE = AB . EF
BC . DE = AB . FD
Solution
BC . DE = AB . EF
स्पष्टीकरण:
हम जानते हैं कि,
यदि एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती हों, और संगत कोण भी बराबर हों, तो त्रिभुज SSS सममिति द्वारा समरूप होते हैं।
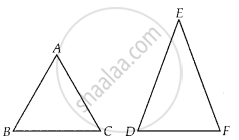
इसलिए, ∆ABC ∼ ∆EDF
समानता संपत्ति का उपयोग करना,
`("AB")/("ED") = ("BC")/("DF") = ("AC")/("EF")`
`("AB")/("ED") = ("BC")/("DF")` लेने पर, हमें प्राप्त होता है।
`("AB")/("ED") = ("BC")/("DF")`
AB . DF = ED . BC
इसलिए, विकल्प (d) BC . DE = AB . FD सत्य है।
`("BC")/("DF") = ("AC")/("EF")` लेने पर, हमें प्राप्त होता है।
`("BC")/("DF") = ("AC")/("EF")`
⇒ BC . EF = AC . DF
इसलिए, विकल्प (a) BC . EF = AC . FD सत्य है।
`("AB")/("ED") = ("AC")/("EF")` लेने पर, हमें प्राप्त होता है।
`("AB")/("ED") = ("AC")/("EF")`
AB . EF = ED . AC
इसलिए, विकल्प (b) AB . EF = AC . DE सत्य है।
APPEARS IN
RELATED QUESTIONS
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
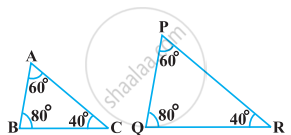
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
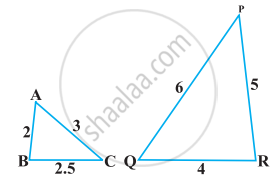
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।