Advertisements
Advertisements
Question
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
Options
ΔPQR ~ ΔCAB
ΔPQR ~ ΔABC
ΔCBA ~ ΔPQR
ΔBCA ~ ΔPQR
Solution
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ΔPQR ~ ΔCAB।
स्पष्टीकरण:
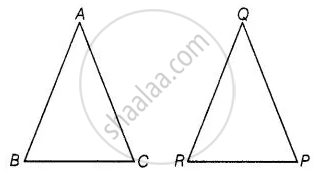
दिया गया है, दो ΔABC और ΔPQR में,
`("AB")/("QR") = ("BC")/("PR") = ("CA")/("PQ")`
जिससे पता चलता है कि एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती होती हैं, फिर उनके संगत कोण भी बराबर होते हैं, इसलिए SSS समरूपता से त्रिभुज समरूप होते हैं।
अर्थात, ΔCAB ∼ ΔPQR
APPEARS IN
RELATED QUESTIONS
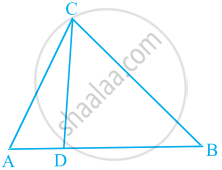
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
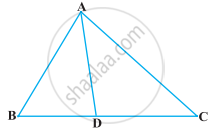
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
क्या यह कहना सत्य है कि यदि दो त्रिभुज में, एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हैं, तो त्रिभुज समरूप होंगे? अपने उत्तर के लिए कारण दीजिए।
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
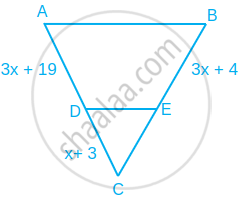
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।