Advertisements
Advertisements
Question
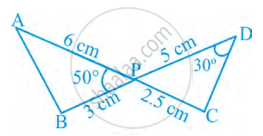
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
Options
50°
30°
60°
100°
Solution
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर 100° है।
स्पष्टीकरण:

∆APB और ∆CPD से,
∠APB = ∠CPD = 50° ...(चूँकि वे शीर्षाभिमुख कोण हैं)
`("AP")/("PD") = 6/5` ...(i)
भी, `("BP")/("CP") = 3/2.5`
या `("BP")/("CP") = 6/5` ...(ii)
समीकरण (i) और (ii) से,
हमें मिलता है,
`("AP")/("PD") = ("BP")/("CP")`
तो, ∆APB ∼ ∆DPC ...[SAS समानता मानदंड का उपयोग करना]
∴ ∠A = ∠D = 30° ...[चूँकि, समरूप त्रिभुजों के संगत कोण]
चूँकि, त्रिभुज के कोणों का योग = 180°,
∆APB में,
∠A + ∠B + ∠APB = 180°
तो, 30° + ∠B + 50° = 180°
फिर, ∠B = 180° – (50° + 30°)
∠B = 180° – 80° = 100°
इसलिए, ∠PBA = 100°
APPEARS IN
RELATED QUESTIONS
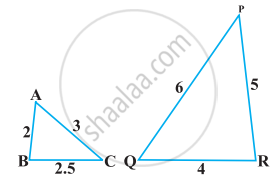
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
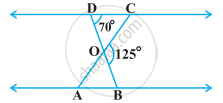
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
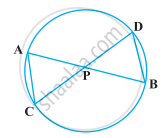
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
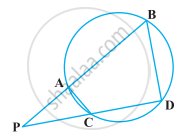
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
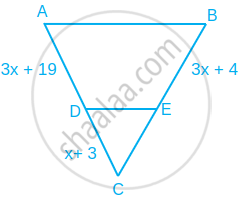
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
ABCD एक समलंब है, जिसमें AB || DC है तथा बिंदु P और Q क्रमश: AD और BC पर इस प्रकार स्थित हैं कि PQ || DC है। यदि PD = 18 cm, BQ = 35 cm और QC = 15 cm है, तो AD ज्ञात कीजिए |
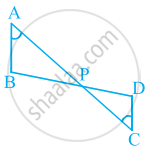
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
यह दिया है कि ΔABC ~ ΔEDF इस प्रकार है कि AB = 5 cm, AC = 7 cm, DF = 15 cm और DE = 12 cm है। इन त्रिभुजों की शेष भुजाओं की लंबाइयाँ ज्ञात कीजिए।
