Advertisements
Advertisements
Question
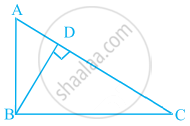
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
Solution
प्रश्न के अनुसार,
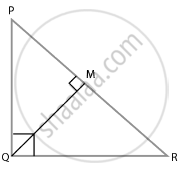
∆PQR में,
PR2 = QR2 और QM ⊥ PR
पाइथागोरस प्रमेय का उपयोग करते हुए, हमारे पास है,
PR2 = PQ2 + QR2
∆PQR, Q पर सही एंगल्ड त्रिभुज है।
∆QMR और ∆PMQ से, हमारे पास है,
∠M = ∠M
∠MQR = ∠QPM ...[= 90° – ∠R]
इसलिए, AAA समानता मानदंड का उपयोग करना,
हमारे पास है,
∆QMR ∼ ∆PMQ
यह भी, हम जानते हैं कि,
त्रिकोणों का क्षेत्र = `1/2` × आधार × ऊँचाई
तो, समान त्रिकोणों के क्षेत्र की संपत्ति द्वारा,
⇒ `("ar(∆QMR)")/("Ar(PMQ)") = ("QM")^2/("PM")^2`
⇒ `("ar(∆QMR)")/("Ar(PMQ)") = (1/2 xx "RM" xx "QM")/(1/2 xx "PM" xx "QM")`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
QM2 = PM × RM
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
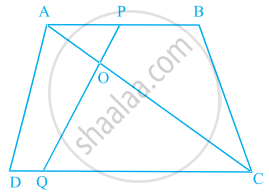
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
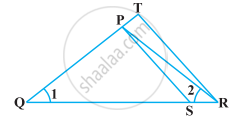
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
सड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।