Advertisements
Advertisements
Question
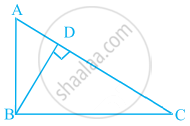
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।
Solution
दिया गया है, ΔABC जिसमें ∠B = 90° और BD ⊥ AC है।
साथ ही, AD = 4 cm और CD = 5 cm
ΔADB और ΔCDB में,
∠ADB = ∠CDB ...[प्रत्येक 90° के बराबर]
और ∠BAD = ∠DBC ...[प्रत्येक 90° – ∠C के बराबर]
∴ ΔDBA ∼ ΔDCB ...[AAA समानता मानदंड द्वारा]
फिर, `("DB")/("DA") = ("DC")/("DB")`
⇒ DB2 = DA × DC
⇒ DB2 = 4 × 5
⇒ DB = `2sqrt(5)` cm
समकोण ∆BDC में,
BC2 = BD2 + CD2 ...[पाइथागोरस प्रमेय द्वारा]
⇒ `"BC"^2 = (2sqrt(5))^2 + (5)^2`
= 20 + 25
= 45
⇒ BC = `sqrt(45) = 3sqrt(5)`
फिर से, ΔDBA ∼ ΔDCB,
∴ `("DB")/("DC") = ("BA")/("BC")`
⇒ `(2sqrt(5))/5 = ("BA")/(3sqrt(5))`
∴ BA = `(2sqrt(5) xx 3sqrt(5))/5` = 6 cm
अतः, BD = `2sqrt(5)` cm और AB = 6 cm।
APPEARS IN
RELATED QUESTIONS
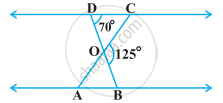
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔADB
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
एक त्रिभुज की दो भुजाओं और परिमाप में से प्रत्येक क्रमश : दूसरे त्रिभुज की संगत दोनों भुजाओं और परिमाप के तिगुने हैं। क्या दोनों त्रिभुज समरूप हैं?
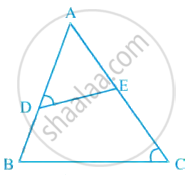
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
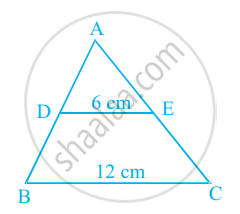
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।