Advertisements
Advertisements
Question
एक त्रिभुज की दो भुजाओं और परिमाप में से प्रत्येक क्रमश : दूसरे त्रिभुज की संगत दोनों भुजाओं और परिमाप के तिगुने हैं। क्या दोनों त्रिभुज समरूप हैं?
Solution
यहाँ, दो त्रिभुजों की संगत दो भुजाएँ और परिमाप समानुपाती हैं, तो दोनों त्रिभुजों की तीसरी भुजा भी समानुपात होगी।
APPEARS IN
RELATED QUESTIONS
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
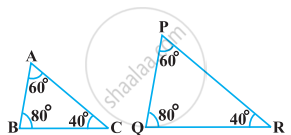
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
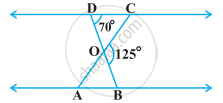
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
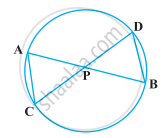
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
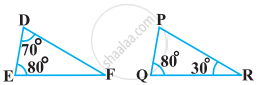
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
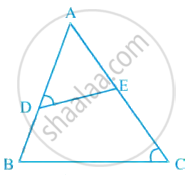
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
