Advertisements
Advertisements
Question
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
Solution
मान लीजिए कि दो समकोण त्रिभुज ∆ABC और ∆PQR हैं।
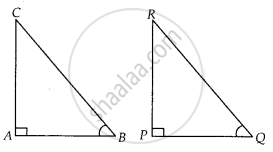
जिसमें, ∠A = ∠P = 90°
और ∠B = ∠Q = न्यून कोण ...(दिया गया है।)
फिर, AA समानता मानदंड से, ∆ABC ~ ∆PQR
APPEARS IN
RELATED QUESTIONS
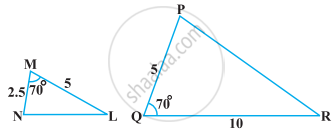
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
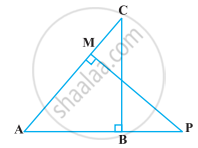
- ΔABC ∼ ΔAMP
- `"CA"/"PA" = "BC"/"MP"`
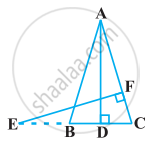
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ∼ ∆ECF है।
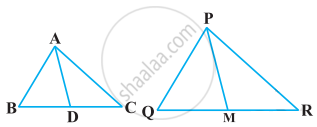
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है (देखिए आकृति)। दर्शाइए कि ∆ABC ∼ ∆PQR है।
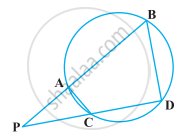
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
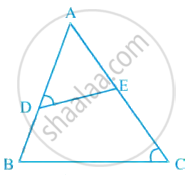
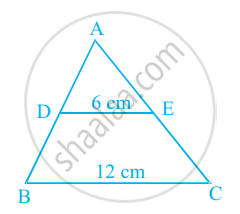
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।