Advertisements
Advertisements
Question
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
Options
∠B = ∠E
∠A = ∠D
∠B = ∠D
∠A = ∠F
Solution
यदि त्रिभुज ABC और DEF में, `("AB")/("DE") = ("BC")/("FD")` है, तो ये समरूप होंगे, जब ∠B = ∠D।
स्पष्टीकरण:
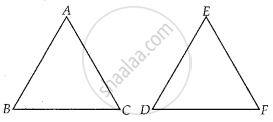
दिया गया है, ∆ABC और ∆EDF में,
`("AB")/("DE") = ("BC")/("FD")`
इसलिए, ∆ABC ~ ∆EDF यदि ∠B = ∠D ...[SAS समरूपता कसौटी के अनुसार]
APPEARS IN
RELATED QUESTIONS
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
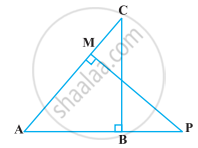
- ΔABC ∼ ΔAMP
- `"CA"/"PA" = "BC"/"MP"`
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
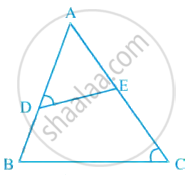
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
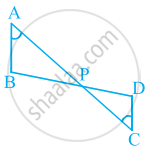
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।