Advertisements
Advertisements
Question
ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm और DF = 7.5 cm दिया हुआ है। तब, निम्नलिखित ______ सत्य है।
Options
DE = 12 cm, ∠F = 50°
DE = 12 cm, ∠F = 100°
EF = 12 cm, ∠D = 100°
EF = 12 cm, ∠D = 30°
Solution
ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm और DF = 7.5 cm दिया हुआ है। तब, निम्नलिखित DE = 12 cm, ∠F = 100° सत्य है।
स्पष्टीकरण:
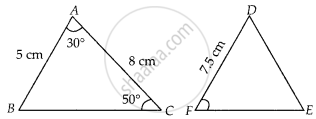
दिया गया है, ∆ABC ~ ∆DFE,
तब ∠A = ∠D = 30°,
∠C = ∠E = 50°
∴ ∠B = ∠F = 180° – (30° + 50°) = 100°
साथ ही, AB = 5 cm,
AC = 8 cm
और DF = 7.5 cm
∴ `("AB")/("DF") = ("AC")/("DE")`
`\implies 5/7.5 = 8/("DE")`
∴ DE = `(8 xx 7.5)/5` = 12 cm
अतः, DE = 12 cm, ∠F = 100°
APPEARS IN
RELATED QUESTIONS
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
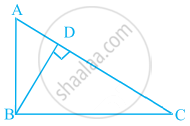
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
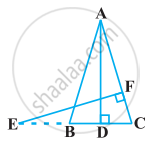
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ∼ ∆ECF है।
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
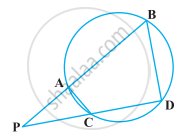
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।