Advertisements
Advertisements
Question
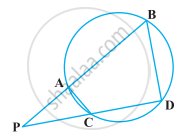
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
Solution
∵ ∠PCA + ∠ACD = 180° …(1) रैखिक युग्म है।
∵ ∠ACD + ∠ABD = 180° ….(2) [चक्रीय चतुर्भुज के सम्मुख कोण]
⇒ ∠PCA = ∠ABD [समीकरण (1) एवं (2) से]
⇒ ∠PCA = ∠PBD …(3) [चित्रानुसार उभयनिष्ठ हैं]
(i) अब APAC एवं APDB में,
∵ ∠PCA = ∠PBD [समीकरण (3) से]
∵ ∠APC = ∠BPD [चित्रानुसार उभयनिष्ठ हैं।
⇒∆PAC ∼ ∆PDB ..........[AA समरूपता]
इति सिद्धम्
(ii) ∵ ∆PAC ∼ ∆PDB [भाग (i) में सिद्ध कर चुके हैं।]
⇒ `"PA"/"PD" = "PC"/"PB"` [समरूप त्रिभुजों के प्रगुण]
⇒ PA.PB = PC.PD.
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
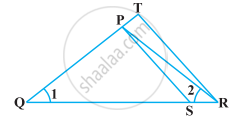
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
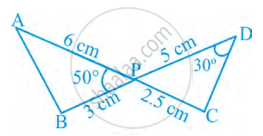
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
