Advertisements
Advertisements
Question
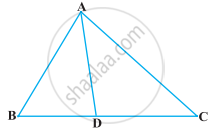
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
Solution
दिया है: ∆ABC की भुजा BC पर बिन्दु D इस प्रकार कि
`"BD"/"CD" = "AB"/"AC"` …(1)
रचना: AD को बढ़ाइए। CE || AD रेखा खींचिए जो AD को बिन्दु E पर प्रतिच्छेद करती है।
अब ∆ABD और ∆ECD में,
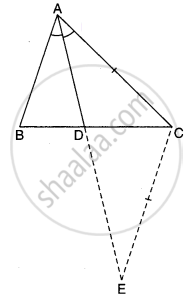
∠ABD = ∠ECD
[AB || CE एवं BD तिर्यक रेखा है।]
∠ADB = ∠EDC [शीर्षाभिमुख कोण है]
∆ABD ∼ ∆ECD [AA समरूपता]
`"BD"/"CD" = "AB"/"EC"` …(2)
[समरूप त्रिभुजों के प्रगुण]
`"AB"/"AC" = "AB"/"EC"`
[समीकरण (1) एवं (2) से]
⇒ AC = EC
⇒ ∠CAD = ∠CED …(3) [बराबर भुजाओं के सम्मुख कोण]
लेकिन ∠BAD = ∠CED …(4) [समरूप ∆ABD एवं ∆ECD के संगत कोण हैं।
∴ ∠BAD = ∠CAD [समीकरण (3) एवं (4) से]
अतः AD कोण BAC का समद्विभाजक है।
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
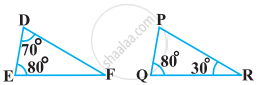
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

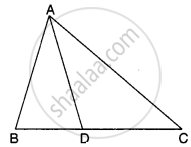
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
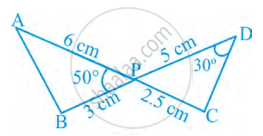
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
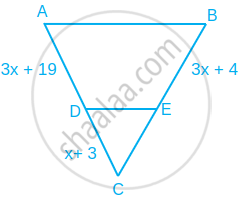
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
सड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
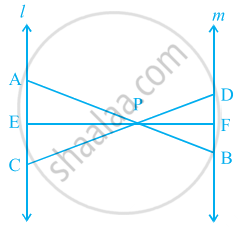
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।