Advertisements
Advertisements
Question
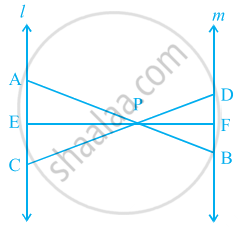
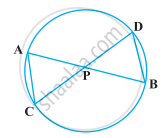
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।
Solution
दिया हुआ, l || m और रेखाखंड AB, CD और EF बिंदु P पर समवर्ती हैं।
साबित करने के लिए: `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
प्रमाण: ΔAPC और ΔBPD में,
∠APC = ∠BPD ...[ऊर्ध्वाधर सम्मुख कोण]
∠PAC = ∠PBD ...[वैकल्पिक कोण]
∴ ΔAPC ∼ ΔBPD ...[AA समानता मानदंड द्वारा]
फिर, `("AP")/("PB") = ("AC")/("BD") = ("PC")/("PD")` ...(i)
ΔAPE और ΔBPF में,
∠APE = ∠BPF ...[ऊर्ध्वाधर विपरीत कोण]
∠PAE = ∠PBF ...[वैकल्पिक कोण]
∴ ΔAPE ∼ ΔBPF ...[AA समानता मानदंड द्वारा]
फिर, `("AP")/("PB") = ("AE")/("BF") = ("PE")/("PF")` ...(ii)
ΔPEC और ΔPFD में,
∠EPC = ∠FPD ...[ऊर्ध्वाधर विपरीत कोण]
∠PCE = ∠PDF ...[वैकल्पिक कोण]
∴ ΔPEC ∼ ΔPFD ...[AA समानता मानदंड द्वारा]
फिर, `("PE")/("PF") = ("PC")/("PD") = ("EC")/("FD")` ...(iii)
समीकरण (i), (ii) और (iii) से,
`("AP")/("PB") = ("AC")/("BD") = ("AE")/("BF") = ("PE")/("PF") = ("EC")/("FD")`
∴ `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
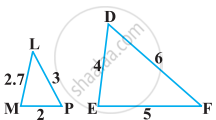
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
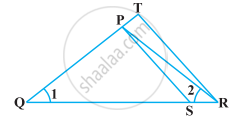
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
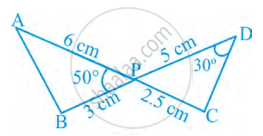
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
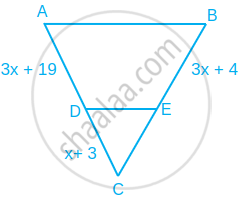
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
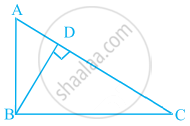
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।