Advertisements
Advertisements
प्रश्न
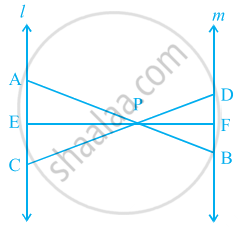
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।
उत्तर
दिया हुआ, l || m और रेखाखंड AB, CD और EF बिंदु P पर समवर्ती हैं।
साबित करने के लिए: `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
प्रमाण: ΔAPC और ΔBPD में,
∠APC = ∠BPD ...[ऊर्ध्वाधर सम्मुख कोण]
∠PAC = ∠PBD ...[वैकल्पिक कोण]
∴ ΔAPC ∼ ΔBPD ...[AA समानता मानदंड द्वारा]
फिर, `("AP")/("PB") = ("AC")/("BD") = ("PC")/("PD")` ...(i)
ΔAPE और ΔBPF में,
∠APE = ∠BPF ...[ऊर्ध्वाधर विपरीत कोण]
∠PAE = ∠PBF ...[वैकल्पिक कोण]
∴ ΔAPE ∼ ΔBPF ...[AA समानता मानदंड द्वारा]
फिर, `("AP")/("PB") = ("AE")/("BF") = ("PE")/("PF")` ...(ii)
ΔPEC और ΔPFD में,
∠EPC = ∠FPD ...[ऊर्ध्वाधर विपरीत कोण]
∠PCE = ∠PDF ...[वैकल्पिक कोण]
∴ ΔPEC ∼ ΔPFD ...[AA समानता मानदंड द्वारा]
फिर, `("PE")/("PF") = ("PC")/("PD") = ("EC")/("FD")` ...(iii)
समीकरण (i), (ii) और (iii) से,
`("AP")/("PB") = ("AC")/("BD") = ("AE")/("BF") = ("PE")/("PF") = ("EC")/("FD")`
∴ `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
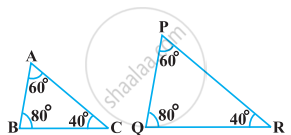
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
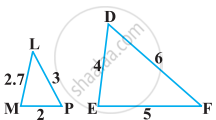
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
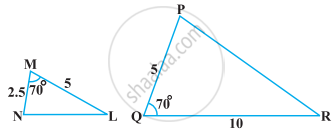
ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm और DF = 7.5 cm दिया हुआ है। तब, निम्नलिखित ______ सत्य है।
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
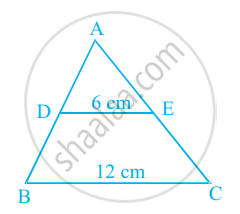
दो समरूप त्रिभुजों की संगत भुजाएँ 2 : 3 के अनुपात में हैं। यदि छोटे त्रिभुज का क्षेत्रफल 48 cm2 है, तो बड़े त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
यह दिया है कि ΔABC ~ ΔEDF इस प्रकार है कि AB = 5 cm, AC = 7 cm, DF = 15 cm और DE = 12 cm है। इन त्रिभुजों की शेष भुजाओं की लंबाइयाँ ज्ञात कीजिए।
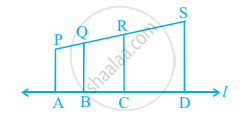
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।