Advertisements
Advertisements
प्रश्न
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
उत्तर
माना मीनार BC = 15 मीटर है और इसकी छाया AB 24 मीटर है।
उस समय ∠CAB = θ.
पुनः, मान लीजिए EF = h एक टेलीफोन खंभा है और उसकी छाया DE = 16 मीटर है।
उसी समय ∠EDF = θ.
यहाँ, ΔASC और ΔDEF दोनों समकोण त्रिभुज हैं।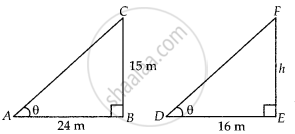
ΔABC और ΔDEF में,
∠CAB = ∠EDF = θ
∠B = ∠E ...[प्रत्येक 90°]
∴ ΔABC ∼ ΔDEF ...[AAA समानता कसौटी द्वारा]
फिर, `("AB")/("DE") = ("BC")/("EF")`
⇒ `24/16 = 15/"h"`
∴ h = `(15 xx 16)/24` = 10
अत:, टेलीफोन के खंभे की ऊँचाई 10 m है।
APPEARS IN
संबंधित प्रश्न
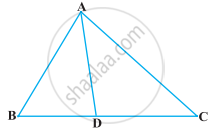
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
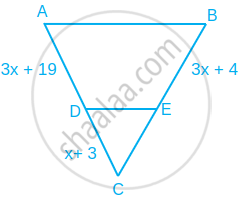
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
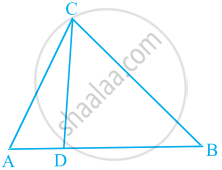
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।
सड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
