Advertisements
Advertisements
प्रश्न
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
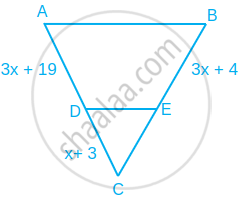
उत्तर
प्रश्न के अनुसार,
DE || AB
आधारभूत समानुपातिकता प्रमेय का प्रयोग करके,
`("CD")/("AD") = ("CE")/("BE")`
∴ यदि एक रेखा को त्रिभुज के एक तरफ के समानांतर खींचा जाता है, तो यह अलग -अलग बिंदुओं पर अन्य पक्षों को काटता है, फिर, अन्य दो पक्षों को एक ही अनुपात में विभाजित किया जाता है।
इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि, खींची गई रेखा त्रिभुज की तीसरी भुजा के बराबर है।
⇒ `(x + 3)/(3x + 19) = x/(3x + 4)`
(x + 3)(3x + 4) = x(3x + 19)
3x2 + 4x + 9x + 12 = 3x2 + 19x
19x – 13x = 12
6x = 12
∴ x = `12/6` = 2
APPEARS IN
संबंधित प्रश्न
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
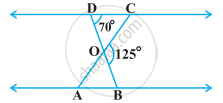
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
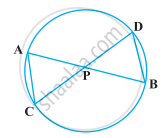
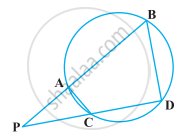
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
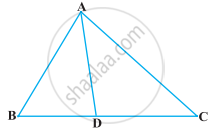
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।
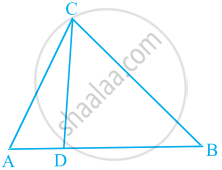
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।