Advertisements
Advertisements
प्रश्न
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
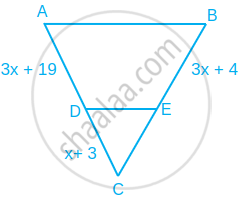
उत्तर
प्रश्न के अनुसार,
DE || AB
आधारभूत समानुपातिकता प्रमेय का प्रयोग करके,
`("CD")/("AD") = ("CE")/("BE")`
∴ यदि एक रेखा को त्रिभुज के एक तरफ के समानांतर खींचा जाता है, तो यह अलग -अलग बिंदुओं पर अन्य पक्षों को काटता है, फिर, अन्य दो पक्षों को एक ही अनुपात में विभाजित किया जाता है।
इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि, खींची गई रेखा त्रिभुज की तीसरी भुजा के बराबर है।
⇒ `(x + 3)/(3x + 19) = x/(3x + 4)`
(x + 3)(3x + 4) = x(3x + 19)
3x2 + 4x + 9x + 12 = 3x2 + 19x
19x – 13x = 12
6x = 12
∴ x = `12/6` = 2
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
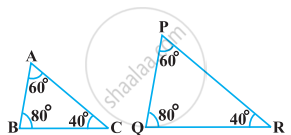
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
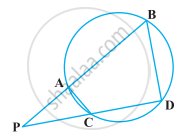
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
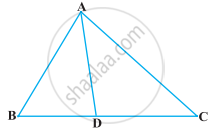
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
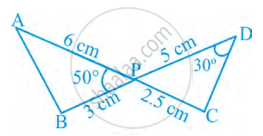
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
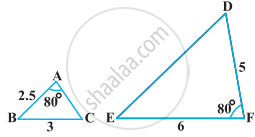
एक त्रिभुज की दो भुजाओं और परिमाप में से प्रत्येक क्रमश : दूसरे त्रिभुज की संगत दोनों भुजाओं और परिमाप के तिगुने हैं। क्या दोनों त्रिभुज समरूप हैं?
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।