Advertisements
Advertisements
Question
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
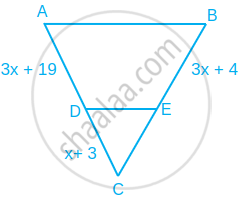
Solution
प्रश्न के अनुसार,
DE || AB
आधारभूत समानुपातिकता प्रमेय का प्रयोग करके,
`("CD")/("AD") = ("CE")/("BE")`
∴ यदि एक रेखा को त्रिभुज के एक तरफ के समानांतर खींचा जाता है, तो यह अलग -अलग बिंदुओं पर अन्य पक्षों को काटता है, फिर, अन्य दो पक्षों को एक ही अनुपात में विभाजित किया जाता है।
इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि, खींची गई रेखा त्रिभुज की तीसरी भुजा के बराबर है।
⇒ `(x + 3)/(3x + 19) = x/(3x + 4)`
(x + 3)(3x + 4) = x(3x + 19)
3x2 + 4x + 9x + 12 = 3x2 + 19x
19x – 13x = 12
6x = 12
∴ x = `12/6` = 2
APPEARS IN
RELATED QUESTIONS
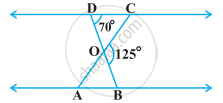
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
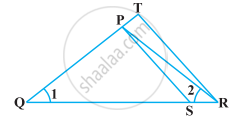
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
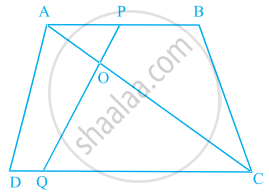
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
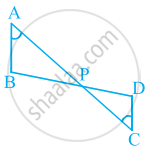
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।