Advertisements
Advertisements
Question
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
Solution
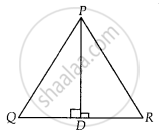
ΔPQD और ΔRPD में,
PD = PD ...[सामान्य पक्ष]
∠PDQ = ∠PDR ...[प्रत्येक 90°]
यहाँ, कोई अन्य भुजाएँ या कोण समान नहीं हैं, इसलिए हम कह सकते हैं कि ∠PQD, ΔRPD के समान नहीं है।
लेकिन, यदि ∠P = 90° है, तो ∠DPQ = ∠PRD
[प्रत्येक 90° – ∠0 के बराबर है और एएसए समानता मानदंड के अनुसार, ΔPQD ~ ΔRPD]
APPEARS IN
RELATED QUESTIONS
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
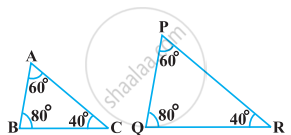
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

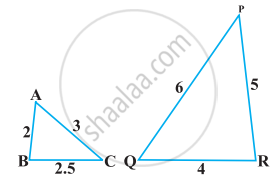
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
दो समरूप त्रिभुजों की संगत भुजाएँ 2 : 3 के अनुपात में हैं। यदि छोटे त्रिभुज का क्षेत्रफल 48 cm2 है, तो बड़े त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
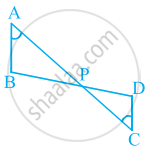
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
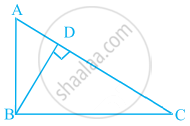
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।