Advertisements
Advertisements
Question
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
Solution 1
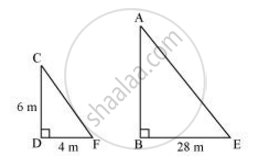
मान लीजिए AB और CD क्रमशः एक मीनार और एक स्तंभ हैं।
मान लीजिए BE और DF की छाया क्रमशः AB और CD की छाया है।
उसी समय, सूर्य से आने वाली प्रकाश किरणें मीनार और स्तंभ पर एक ही कोण पर पड़ेंगी।
इसलिए, ∠DCF = ∠BAE
और, ∠DFC = ∠BEA
∠CDF = ∠ABE ...(मीनार और स्तंभ जमीन से लंबवत हैं)
∴ ΔABE ∼ ΔCDF ...(AAA समरूपता कसौटी)
⇒ `("AB")/("CB") = ("BE")/("DF")`
⇒ `("AB")/(6"m") = 28/4`
⇒ AB = 42 m
इसलिए, मीनार की ऊंचाई 42 मीटर होगी।
Solution 2
(a)
(b)
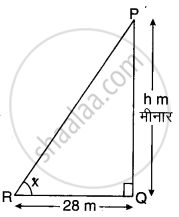
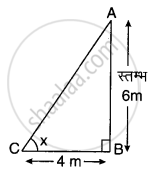
मान लीजिए AB = 6 cm लम्बा एक स्तम्भ है जिसकी छाया BC की लम्बाई 4 m है एवं ∠ABC = 90° तथा ∠C = x° है। आकृति एवं PQ = h m (मान लीजिए) कि मीनार की छाया QR की लम्बाई 28 m है एवं ∠PQR = 90° तथा ∠R = x° है।
∠C = ∠R = x° (सूर्य का उन्नयन कोण) एवं ∠B = ∠Q = 90°
∆ABC ∼ ∆PQR ...[AA समरूपता]
⇒ `"AB"/"BC" = "PQ"/"QR"` ...[समरूप त्रिभुज के प्रगुण]
⇒ `6/4 = "h"/28`
⇒ h = `6/4 xx 28`
⇒ h = 42 m
अत: मीनार की अभीष्ट ऊँचाई = 42 cm है।
APPEARS IN
RELATED QUESTIONS
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
क्या यह कहना सत्य है कि यदि दो त्रिभुज में, एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हैं, तो त्रिभुज समरूप होंगे? अपने उत्तर के लिए कारण दीजिए।
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

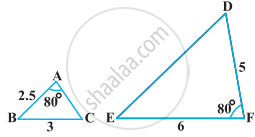
ABCD एक समलंब है, जिसमें AB || DC है तथा बिंदु P और Q क्रमश: AD और BC पर इस प्रकार स्थित हैं कि PQ || DC है। यदि PD = 18 cm, BQ = 35 cm और QC = 15 cm है, तो AD ज्ञात कीजिए |
