Advertisements
Advertisements
प्रश्न
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
उत्तर १
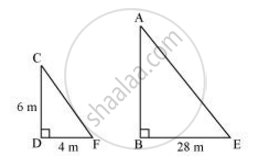
मान लीजिए AB और CD क्रमशः एक मीनार और एक स्तंभ हैं।
मान लीजिए BE और DF की छाया क्रमशः AB और CD की छाया है।
उसी समय, सूर्य से आने वाली प्रकाश किरणें मीनार और स्तंभ पर एक ही कोण पर पड़ेंगी।
इसलिए, ∠DCF = ∠BAE
और, ∠DFC = ∠BEA
∠CDF = ∠ABE ...(मीनार और स्तंभ जमीन से लंबवत हैं)
∴ ΔABE ∼ ΔCDF ...(AAA समरूपता कसौटी)
⇒ `("AB")/("CB") = ("BE")/("DF")`
⇒ `("AB")/(6"m") = 28/4`
⇒ AB = 42 m
इसलिए, मीनार की ऊंचाई 42 मीटर होगी।
उत्तर २
(a)
(b)
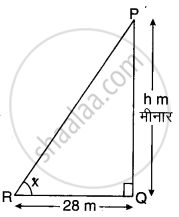
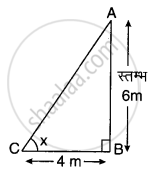
मान लीजिए AB = 6 cm लम्बा एक स्तम्भ है जिसकी छाया BC की लम्बाई 4 m है एवं ∠ABC = 90° तथा ∠C = x° है। आकृति एवं PQ = h m (मान लीजिए) कि मीनार की छाया QR की लम्बाई 28 m है एवं ∠PQR = 90° तथा ∠R = x° है।
∠C = ∠R = x° (सूर्य का उन्नयन कोण) एवं ∠B = ∠Q = 90°
∆ABC ∼ ∆PQR ...[AA समरूपता]
⇒ `"AB"/"BC" = "PQ"/"QR"` ...[समरूप त्रिभुज के प्रगुण]
⇒ `6/4 = "h"/28`
⇒ h = `6/4 xx 28`
⇒ h = 42 m
अत: मीनार की अभीष्ट ऊँचाई = 42 cm है।
APPEARS IN
संबंधित प्रश्न
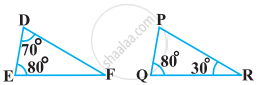
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
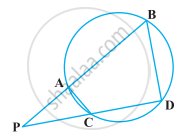
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
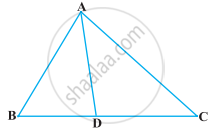
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
क्या यह कहना सत्य है कि यदि दो त्रिभुज में, एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हैं, तो त्रिभुज समरूप होंगे? अपने उत्तर के लिए कारण दीजिए।
समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
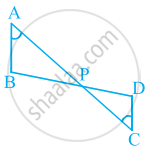
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।