Advertisements
Advertisements
प्रश्न
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
विकल्प
BC . EF = A C. FD
AB . EF = AC . DE
BC . DE = AB . EF
BC . DE = AB . FD
उत्तर
BC . DE = AB . EF
स्पष्टीकरण:
हम जानते हैं कि,
यदि एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती हों, और संगत कोण भी बराबर हों, तो त्रिभुज SSS सममिति द्वारा समरूप होते हैं।
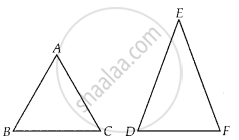
इसलिए, ∆ABC ∼ ∆EDF
समानता संपत्ति का उपयोग करना,
`("AB")/("ED") = ("BC")/("DF") = ("AC")/("EF")`
`("AB")/("ED") = ("BC")/("DF")` लेने पर, हमें प्राप्त होता है।
`("AB")/("ED") = ("BC")/("DF")`
AB . DF = ED . BC
इसलिए, विकल्प (d) BC . DE = AB . FD सत्य है।
`("BC")/("DF") = ("AC")/("EF")` लेने पर, हमें प्राप्त होता है।
`("BC")/("DF") = ("AC")/("EF")`
⇒ BC . EF = AC . DF
इसलिए, विकल्प (a) BC . EF = AC . FD सत्य है।
`("AB")/("ED") = ("AC")/("EF")` लेने पर, हमें प्राप्त होता है।
`("AB")/("ED") = ("AC")/("EF")`
AB . EF = ED . AC
इसलिए, विकल्प (b) AB . EF = AC . DE सत्य है।
APPEARS IN
संबंधित प्रश्न
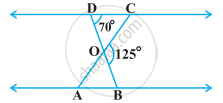
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
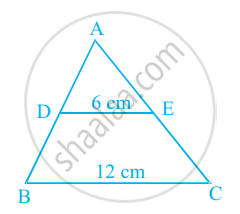
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
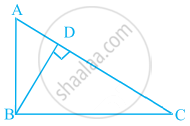
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।
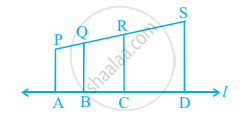
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।