Advertisements
Advertisements
प्रश्न
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
विकल्प
ΔPQR ~ ΔCAB
ΔPQR ~ ΔABC
ΔCBA ~ ΔPQR
ΔBCA ~ ΔPQR
उत्तर
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ΔPQR ~ ΔCAB।
स्पष्टीकरण:
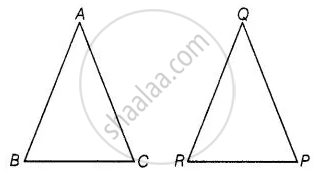
दिया गया है, दो ΔABC और ΔPQR में,
`("AB")/("QR") = ("BC")/("PR") = ("CA")/("PQ")`
जिससे पता चलता है कि एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती होती हैं, फिर उनके संगत कोण भी बराबर होते हैं, इसलिए SSS समरूपता से त्रिभुज समरूप होते हैं।
अर्थात, ΔCAB ∼ ΔPQR
APPEARS IN
संबंधित प्रश्न
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ∼ ∆FEG है, तो दर्शाइए कि:
- `"CD"/"GH" = "AC"/"FG"`
- ∆DCB ∼ ∆HGE
- ∆DCA ∼ ∆HGF
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
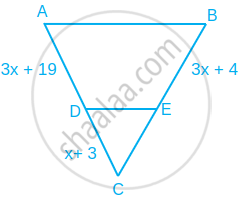
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
