Advertisements
Advertisements
प्रश्न
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
उत्तर
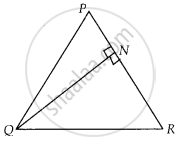
दिया गया है, ∆PQR,
N, PR पर एक बिंदु है, इस प्रकार कि QN ⊥ PR
और PN . NR = QN2
सिद्ध करना है: ∠PQR = 90°
प्रमाण: हमारे पास है, PN . NR = QN2
⇒ PN . NR = QN . QN
⇒ `("PN")/("QN") = ("QN")/("NR")` ...(i)
∆QNP और ∆RNQ में,
`("PN")/("QN") = ("QN")/("NR")`
और ∠PNQ = ∠RNQ ...[प्रत्येक 90° के बराबर]
∴ ∆QNP ~ ∆RNQ ...[SAS समानता मानदंड द्वारा]
फिर, ∆QNP और ∆RNQ समबाहु हैं।
अर्थात, ∠PQN = ∠QRN
⇒ ∠RQN = ∠QPN
दोनों पक्षों को जोड़ने पर, हमें प्राप्त होता है
∠PQN + ∠RQN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN ...(ii)
हम जानते हैं कि, त्रिभुज के कोणों का योग 180° होता है।
In ∆PQR,
∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + ∠QPN + ∠QRN = 180° ...[∵ ∠QPR = ∠QPN और ∠QRP = ∠QRN]
⇒ ∠PQR + ∠PQR = 180° ...[समीकरण (ii) का प्रयोग]
⇒ 2∠PQR = 180°
⇒ ∠PQR = `180^circ/2` = 90°
∴ ∠PQR = 90°
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
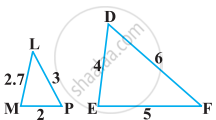
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
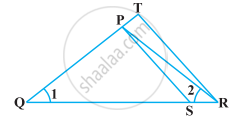
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
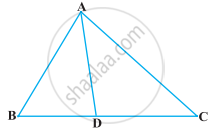
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
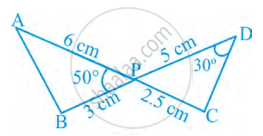
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
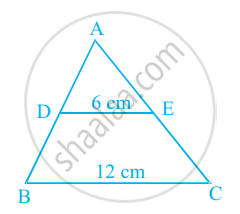
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
सड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
