Advertisements
Advertisements
Question
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
Solution
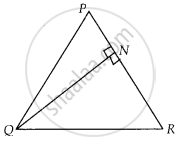
दिया गया है, ∆PQR,
N, PR पर एक बिंदु है, इस प्रकार कि QN ⊥ PR
और PN . NR = QN2
सिद्ध करना है: ∠PQR = 90°
प्रमाण: हमारे पास है, PN . NR = QN2
⇒ PN . NR = QN . QN
⇒ `("PN")/("QN") = ("QN")/("NR")` ...(i)
∆QNP और ∆RNQ में,
`("PN")/("QN") = ("QN")/("NR")`
और ∠PNQ = ∠RNQ ...[प्रत्येक 90° के बराबर]
∴ ∆QNP ~ ∆RNQ ...[SAS समानता मानदंड द्वारा]
फिर, ∆QNP और ∆RNQ समबाहु हैं।
अर्थात, ∠PQN = ∠QRN
⇒ ∠RQN = ∠QPN
दोनों पक्षों को जोड़ने पर, हमें प्राप्त होता है
∠PQN + ∠RQN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN ...(ii)
हम जानते हैं कि, त्रिभुज के कोणों का योग 180° होता है।
In ∆PQR,
∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + ∠QPN + ∠QRN = 180° ...[∵ ∠QPR = ∠QPN और ∠QRP = ∠QRN]
⇒ ∠PQR + ∠PQR = 180° ...[समीकरण (ii) का प्रयोग]
⇒ 2∠PQR = 180°
⇒ ∠PQR = `180^circ/2` = 90°
∴ ∠PQR = 90°
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
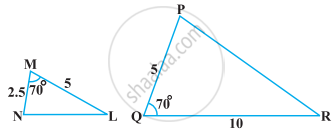
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
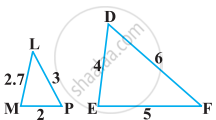
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔADB
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
त्रिभुजों PQR और MST में, ∠P = 55°, ∠Q = 25°, ∠M = 100° और ∠S = 25° है। क्या ∆QPR ~ ∆TSM है? क्यों?
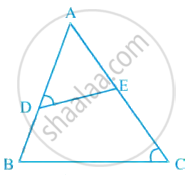
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
दो समरूप त्रिभुजों के क्षेत्रफल 36 cm2 और 100 cm2 हैं। यदि बड़े त्रिभुज की एक भुजा की लंबाई 20 cm है, तो उस भुजा के संगत छोटे त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
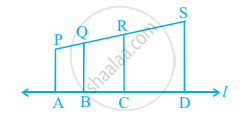
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।