Advertisements
Advertisements
Question
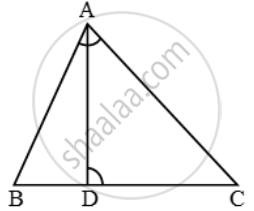
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
Solution
∆ABC और ∆DAC में, हमारे पास है
∠ADC = ∠BAC और ∠C = ∠C
इसलिए, समरूपता के AA-कसौटी से, हमारे पास है
∆ABC ~ ∆DAC
`\Rightarrow \frac{"AB"}{"DA"}=\frac{"BC"}{"AC"}=\frac{"AC"}{"DC"}`
`\Rightarrow \frac{"CB"}{"CA"}=\frac{"CA"}{"CD"}`
APPEARS IN
RELATED QUESTIONS
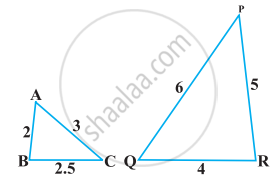
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
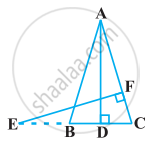
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ∼ ∆ECF है।
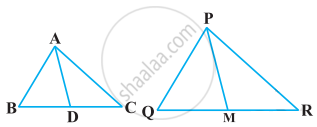
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है (देखिए आकृति)। दर्शाइए कि ∆ABC ∼ ∆PQR है।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
क्या यह कहना सत्य है कि यदि दो त्रिभुज में, एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हैं, तो त्रिभुज समरूप होंगे? अपने उत्तर के लिए कारण दीजिए।
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
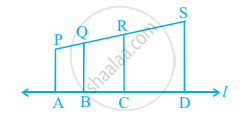
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।