Advertisements
Advertisements
प्रश्न
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
विकल्प
सर्वांगसम परंतु समरूप नहीं
समरूप परंतु सर्वांगसम नहीं
न तो सर्वांगसम और न ही समरूप
सर्वांगसम और समरूप दोनों
उत्तर
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज समरूप परंतु सर्वांगसम नहीं हैं।
स्पष्टीकरण:
∆ABC और ∆DEF में,
∠B = ∠E,
∠F = ∠C
और AB = 3DE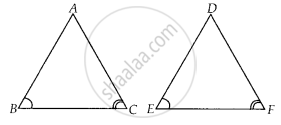
हम जानते हैं कि,
यदि दो त्रिभुजों में संगत दो कोण समान हैं, तो वे AA समानता मानदंड के अनुसार समान हैं।
चूँकि, AB ≠ DE
इसलिए ∆ABC और ∆DEF सर्वांगसम नहीं हैं।
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
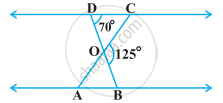
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔADB
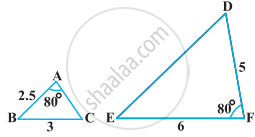
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
एक त्रिभुज की दो भुजाओं और परिमाप में से प्रत्येक क्रमश : दूसरे त्रिभुज की संगत दोनों भुजाओं और परिमाप के तिगुने हैं। क्या दोनों त्रिभुज समरूप हैं?
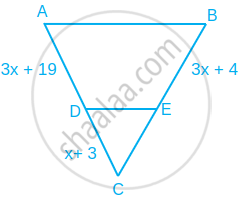
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।