Advertisements
Advertisements
प्रश्न
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
उत्तर
दिया गया है, ΔABC ∼ ΔPQR
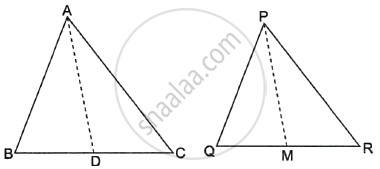
⇒ `("AB")/("PQ") = ("BC")/("QR") = ("AC")/("PR")`
(समान त्रिभुजों के भुजा-अनुपात गुण से)
⇒ ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ...(i)
BC = 2BD और QR = 2QM ...(∵ P और M BC और QR के मध्यबिंदु हैं)
⇒ `("AB")/("PQ") = (2 "BD")/(2 "QM") = ("AC")/("PR")`
⇒ `("AB")/("PQ") = ("BD")/("QM") = ("AC")/("PR")` ...(ii)
अब ΔABD और ΔPQM में
`("AB")/("PQ") = ("BD")/("QM")` ...((ii) से)
∠B = ∠Q ...((i) से)
⇒ ΔABD ∼ ΔPQM ...(SAS समरूपता कसौटी)
∴ `("AB")/("PQ") = ("AD")/("PM")`
अतः, सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
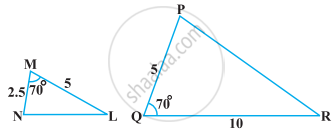
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm और DF = 7.5 cm दिया हुआ है। तब, निम्नलिखित ______ सत्य है।
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
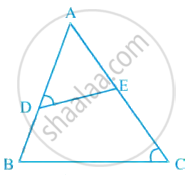
आकृति में, यदि ∠D = ∠C है, तो क्या यह सत्य है कि ΔADE ~ ΔACB है? क्यों?
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
ABCD एक समलंब है, जिसमें AB || DC है तथा बिंदु P और Q क्रमश: AD और BC पर इस प्रकार स्थित हैं कि PQ || DC है। यदि PD = 18 cm, BQ = 35 cm और QC = 15 cm है, तो AD ज्ञात कीजिए |
