Advertisements
Advertisements
प्रश्न
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
उत्तर
प्रश्न के अनुसार,
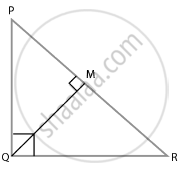
∆PQR में,
PR2 = QR2 और QM ⊥ PR
पाइथागोरस प्रमेय का उपयोग करते हुए, हमारे पास है,
PR2 = PQ2 + QR2
∆PQR, Q पर सही एंगल्ड त्रिभुज है।
∆QMR और ∆PMQ से, हमारे पास है,
∠M = ∠M
∠MQR = ∠QPM ...[= 90° – ∠R]
इसलिए, AAA समानता मानदंड का उपयोग करना,
हमारे पास है,
∆QMR ∼ ∆PMQ
यह भी, हम जानते हैं कि,
त्रिकोणों का क्षेत्र = `1/2` × आधार × ऊँचाई
तो, समान त्रिकोणों के क्षेत्र की संपत्ति द्वारा,
⇒ `("ar(∆QMR)")/("Ar(PMQ)") = ("QM")^2/("PM")^2`
⇒ `("ar(∆QMR)")/("Ar(PMQ)") = (1/2 xx "RM" xx "QM")/(1/2 xx "PM" xx "QM")`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
QM2 = PM × RM
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
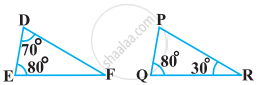
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
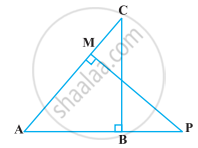
- ΔABC ∼ ΔAMP
- `"CA"/"PA" = "BC"/"MP"`
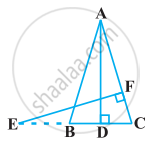
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ∼ ∆ECF है।
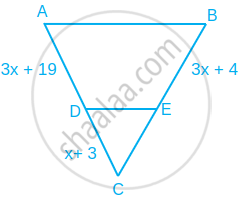
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
यदि त्रिभुज ABC और DEF में, `(AB)/(DE) = (BC)/(FD)` है, तो ये समरूप होंगे, जब ______।
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
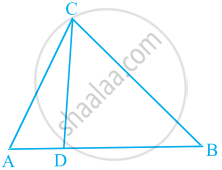
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।