Advertisements
Advertisements
प्रश्न
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
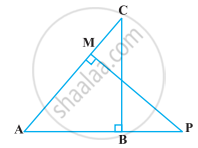
- ΔABC ∼ ΔAMP
- `"CA"/"PA" = "BC"/"MP"`
उत्तर
(i) ΔABC और ΔAMP में,
∠ABC = ∠AMP ...(प्रत्येक 90°)
∠A = ∠A ...(सामान्य)
∴ ΔABC ∼ ΔAMP ...(AA समरूपता कसौटी द्वारा)
(ii) हमारे पास है,
∠B = ∠M = 90°
और, ∠BAC = ∠MAP
ΔABC और ΔAMP में
∠B = ∠M ...[प्रत्येक 90°]
∠BAC = ∠MAP ...[दिया गया है]
फिर, ΔABC ~ ΔAMP ....[AA समरूपता से]
∴ `"CA"/"PA"="BC"/"MP"` ....[समान Δ के संगत भाग समानुपातिक होते हैं]
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
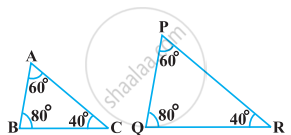
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
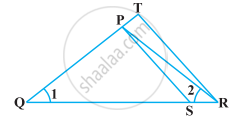
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
त्रिभुजों PQR और MST में, ∠P = 55°, ∠Q = 25°, ∠M = 100° और ∠S = 25° है। क्या ∆QPR ~ ∆TSM है? क्यों?
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
ABCD एक समलंब है, जिसमें AB || DC है तथा बिंदु P और Q क्रमश: AD और BC पर इस प्रकार स्थित हैं कि PQ || DC है। यदि PD = 18 cm, BQ = 35 cm और QC = 15 cm है, तो AD ज्ञात कीजिए |
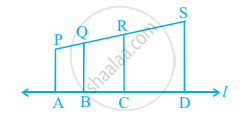
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।