Advertisements
Advertisements
प्रश्न
त्रिभुजों PQR और MST में, ∠P = 55°, ∠Q = 25°, ∠M = 100° और ∠S = 25° है। क्या ∆QPR ~ ∆TSM है? क्यों?
उत्तर
हम जानते हैं कि, एक त्रिभुज के तीन कोणों का योग 180° होता है।

∆PQR में,
∠P + ∠Q + ∠R = 180°
⇒ 55° + 25 ° + ∠R = 180°
⇒∠R = 180° – (55° + 25°)
= 180° – 80°
= 100°
∆TSM में,
∠T + ∠S + ∠M = 180°
⇒ ∠T + ∠25° + 100° = 180°
⇒ ∠T = 180° – (25° + 100°)
= 180° – 125°
= 55°
∆PQR और ∆TSM में,
∠P = ∠T,
∠Q = ∠S
और ∠R = ∠M
∴ ∠PQR = ∠TSM ...[चूँकि, सभी संगत कोण बराबर होते हैं।]
इसलिए, ∆QPR, ∆TSM के समान नहीं है, क्योंकि सही संगति P `↔` T, Q `↔` S और R `↔` M है।
APPEARS IN
संबंधित प्रश्न
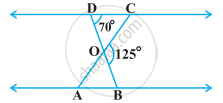
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
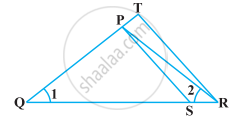
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
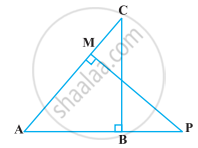
- ΔABC ∼ ΔAMP
- `"CA"/"PA" = "BC"/"MP"`
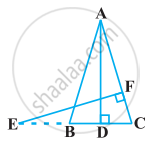
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ∆ABD ∼ ∆ECF है।
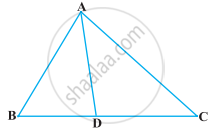
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
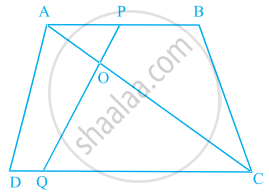
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
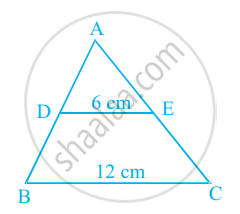
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
यह दिया है कि ΔABC ~ ΔEDF इस प्रकार है कि AB = 5 cm, AC = 7 cm, DF = 15 cm और DE = 12 cm है। इन त्रिभुजों की शेष भुजाओं की लंबाइयाँ ज्ञात कीजिए।
