Advertisements
Advertisements
प्रश्न
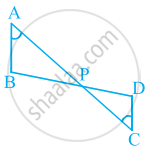
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
उत्तर
प्रश्न के अनुसार,
AC और PQ परस्पर बिंदु O और AB || DC पर प्रतिच्छेद करते हैं।
∆AOP और ∆COQ से,
∠AOP = ∠COQ ...[चूंकि वे लंबवत विपरीत कोण हैं]
∠APO = ∠CQO ...[चूँकि AB || DC और PQ तिर्यक रेखा है, कोण एकांतर कोण हैं]
∴ ∆AOP ∼ ∆COQ ...[AAA समानता मानदंड का उपयोग करके]
तब, चूँकि संगत भुजाएँ समानुपाती होती हैं।
हमारे पास है,
`("OA")/("OC") = ("AP")/("CQ")`
OA × CQ = OC × AP
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
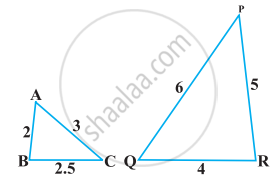
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
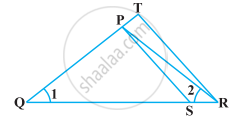
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
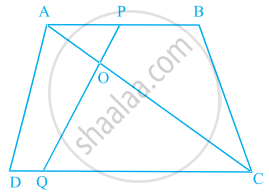
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
एक त्रिभुज की दो भुजाओं और परिमाप में से प्रत्येक क्रमश : दूसरे त्रिभुज की संगत दोनों भुजाओं और परिमाप के तिगुने हैं। क्या दोनों त्रिभुज समरूप हैं?
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।