Advertisements
Advertisements
प्रश्न
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
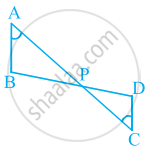
उत्तर
प्रश्न के अनुसार,
∠A = ∠C,
AB = 6 cm,
BP = 15 cm,
AP = 12 cm
CP = 4 cm
∆APB और ∆CPD से,
∠A = ∠C
∠APB = ∠CPD ...[लंबवत विपरीत कोण]
∴ AAA समानता मानदंड द्वारा,
ΔAPD ∼ ΔCPD
मूल आनुपातिकता प्रमेय का उपयोग करना,
⇒ `("AP")/("CP") = ("PB")/("PD") = ("AB")/("CD")` ...[मूल आनुपातिकता प्रमेय द्वारा]
⇒ `12/4 = 15/("PD") = 6/("CD")`
`("AP")/("CP") = ("PB")/("PD")`, पर विचार करते हुए, हम प्राप्त करते हैं,
`12/4 = 15/("PD")`
PD = `(15 xx 4)/12`
= `60/12`
= 5 cm
विचार करते हुए, `("AP")/("CP") = ("AB")/("CD")`
⇒ `"CD" = ((6 xx 4))/12` = 2 cm
इसलिए,
PD की लंबाई = 5 cm
CD की लंबाई = 2 cm
APPEARS IN
संबंधित प्रश्न
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
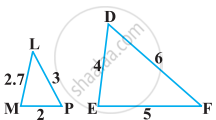
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ∼ ∆FEG है, तो दर्शाइए कि:
- `"CD"/"GH" = "AC"/"FG"`
- ∆DCB ∼ ∆HGE
- ∆DCA ∼ ∆HGF
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
एक त्रिभुज की दो भुजाओं और परिमाप में से प्रत्येक क्रमश : दूसरे त्रिभुज की संगत दोनों भुजाओं और परिमाप के तिगुने हैं। क्या दोनों त्रिभुज समरूप हैं?
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
