Advertisements
Advertisements
प्रश्न
आकृति में, यदि ∠1 = ∠2 और ΔNSQ ≅ ΔMTR है, तो सिद्ध कीजिए ΔPTS ~ ΔPRQ है।

उत्तर
प्रश्न के अनुसार,
ΔNSQ ≅ ΔMTR
∠1 = ∠2
चूंकि,
∆NSQ = ∆MTR
तो,
SQ = TR ...(i)
भी,
∠1 = ∠2 ⇒ PT = PS ...(ii) [चूंकि, समान कोणों के विपरीत पक्ष भी समान हैं।]
समीकरण (i) और (ii) से,
`("PS")/("SQ") = ("PT")/("TR")`
⇒ ST || QR
आधारभूत समानुपातिकता प्रमेय के व्युत्क्रम से, यदि एक त्रिभुज की एक भुजा के समांतर अन्य भुजाओं को अलग-अलग बिंदुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाती है, तो अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
∴ ∠1 = PQR
और
∠2 = ∠PRQ
∆PTS और ∆PRQ में,
∠P = ∠P ...[उभयनिष्ठ कोण]
∠1 = ∠PQR ...(सिद्ध)
∠2 = ∠PRQ ...(सिद्ध)
∴ ∆PTS – ∆PRQ ...[AAA समानता मानदंड द्वारा]
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ∼ ∆FEG है, तो दर्शाइए कि:
- `"CD"/"GH" = "AC"/"FG"`
- ∆DCB ∼ ∆HGE
- ∆DCA ∼ ∆HGF
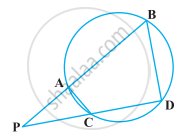
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
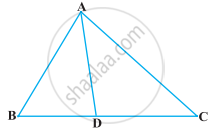
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
क्या यह कहना सत्य है कि यदि दो त्रिभुज में, एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर है तथा एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हैं, तो त्रिभुज समरूप होंगे? अपने उत्तर के लिए कारण दीजिए।
∆PQR में, PR2 – PQ2 = QR2 है तथा M भुजा PR पर एक बिंदु इस प्रकार स्थित है कि QM⊥ PR है। सिद्ध कीजिए कि QM2 = PM × MR है।
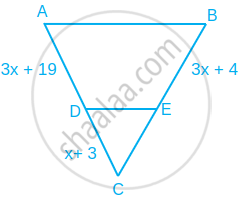
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
सड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
