Advertisements
Advertisements
प्रश्न
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
उत्तर
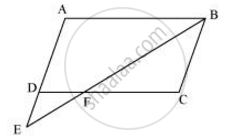
In ΔABE and ΔCFB,
∠BAE = ∠FCB ...(समानांतर चतुर्भुज के विपरीत कोण)
∠AEB = ∠CBF ...(AE || BC के रूप में वैकल्पिक आंतरिक कोण)
∴ ΔABE ∼ ΔCFB ...(AA समरूपता कसौटी के अनुसार)
APPEARS IN
संबंधित प्रश्न
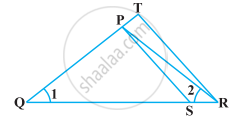
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔABD ∼ ΔCBE
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔADB
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
यदि दो समकोण त्रिभुजों में एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
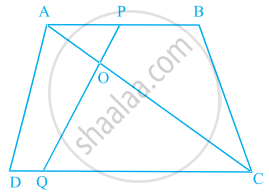
ABCD एक समलंब है, जिसमें AB || DC है तथा बिंदु P और Q क्रमश: AD और BC पर इस प्रकार स्थित हैं कि PQ || DC है। यदि PD = 18 cm, BQ = 35 cm और QC = 15 cm है, तो AD ज्ञात कीजिए |
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।