Advertisements
Advertisements
Question
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
Solution
दिया गया है, ΔABC ∼ ΔPQR
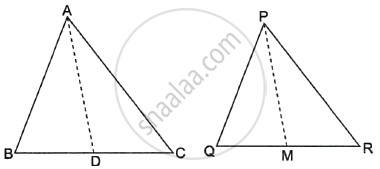
⇒ `("AB")/("PQ") = ("BC")/("QR") = ("AC")/("PR")`
(समान त्रिभुजों के भुजा-अनुपात गुण से)
⇒ ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ...(i)
BC = 2BD और QR = 2QM ...(∵ P और M BC और QR के मध्यबिंदु हैं)
⇒ `("AB")/("PQ") = (2 "BD")/(2 "QM") = ("AC")/("PR")`
⇒ `("AB")/("PQ") = ("BD")/("QM") = ("AC")/("PR")` ...(ii)
अब ΔABD और ΔPQM में
`("AB")/("PQ") = ("BD")/("QM")` ...((ii) से)
∠B = ∠Q ...((i) से)
⇒ ΔABD ∼ ΔPQM ...(SAS समरूपता कसौटी)
∴ `("AB")/("PQ") = ("AD")/("PM")`
अतः, सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
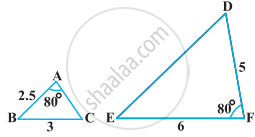
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
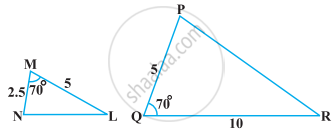
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
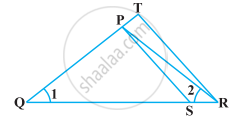
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
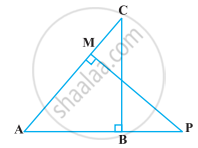
- ΔABC ∼ ΔAMP
- `"CA"/"PA" = "BC"/"MP"`
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
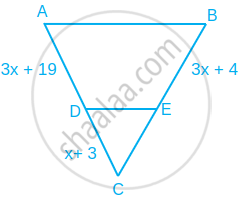
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
समलंब PQRS के विकर्ण परस्पर O पर प्रतिच्छेद करते हैं, PQ || RS और PQ = 3 RS हैं। त्रिभुजों POQ और ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
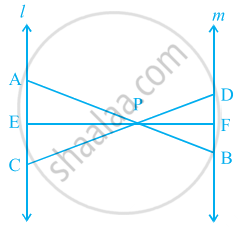
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।