Advertisements
Advertisements
Question
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
Options
`("EF")/("PR") = ("DF")/("PQ")`
`("DE")/("PQ") = ("EF")/("RP")`
`("DE")/("QR") = ("DF")/("PQ")`
`("EF")/("RP") = ("DE")/("QR")`
Solution
`bb((DE)/(PQ) = (EF)/(RP))`
स्पष्टीकरण:
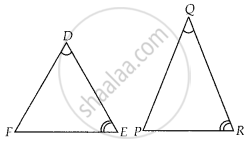
दिया गया है, ∆DEF और ∆PQR में,
∠D = ∠Q,
∠R = ∠E
∴ ∆DEF ~ ∆QRP ...[AAA समानता मानदंड द्वारा]
⇒ ∠F = ∠P ...[समान त्रिभुजों के संगत कोण]
∴ `("DF")/("QP") = ("ED")/("RQ") = ("FE")/("PR")`
APPEARS IN
RELATED QUESTIONS
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ∼ ∆FEG है, तो दर्शाइए कि:
- `"CD"/"GH" = "AC"/"FG"`
- ∆DCB ∼ ∆HGE
- ∆DCA ∼ ∆HGF
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
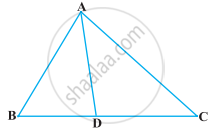
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
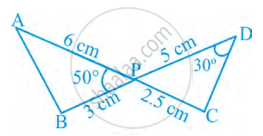
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm और DF = 7.5 cm दिया हुआ है। तब, निम्नलिखित ______ सत्य है।
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
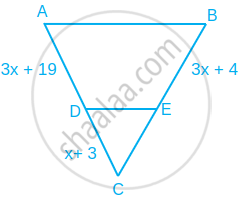
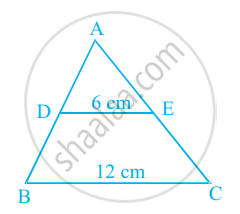
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
दो समरूप त्रिभुजों के क्षेत्रफल 36 cm2 और 100 cm2 हैं। यदि बड़े त्रिभुज की एक भुजा की लंबाई 20 cm है, तो उस भुजा के संगत छोटे त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
