Advertisements
Advertisements
प्रश्न
एक विशेष समय पर, 15 मीटर ऊँची एक मीनार (टॉवर) की छाया की लंबाई 24 मीटर है। उसी समय पर, एक टेलीफोन के खंभे की छाया की लंबाई 16 मीटर है। टेलीफोन के खंभे की ऊँचाई ज्ञात कीजिए।
उत्तर
माना मीनार BC = 15 मीटर है और इसकी छाया AB 24 मीटर है।
उस समय ∠CAB = θ.
पुनः, मान लीजिए EF = h एक टेलीफोन खंभा है और उसकी छाया DE = 16 मीटर है।
उसी समय ∠EDF = θ.
यहाँ, ΔASC और ΔDEF दोनों समकोण त्रिभुज हैं।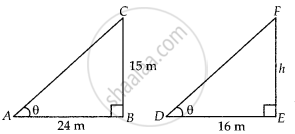
ΔABC और ΔDEF में,
∠CAB = ∠EDF = θ
∠B = ∠E ...[प्रत्येक 90°]
∴ ΔABC ∼ ΔDEF ...[AAA समानता कसौटी द्वारा]
फिर, `("AB")/("DE") = ("BC")/("EF")`
⇒ `24/16 = 15/"h"`
∴ h = `(15 xx 16)/24` = 10
अत:, टेलीफोन के खंभे की ऊँचाई 10 m है।
APPEARS IN
संबंधित प्रश्न
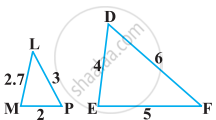
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
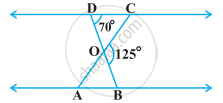
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
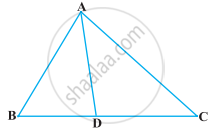
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
यदि ΔABC ~ ΔEDF और ΔABC, ΔDEF के समरूप नहीं है, तो निम्नलिखित से कौन सत्य नहीं है?
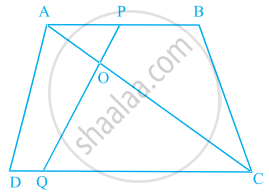
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
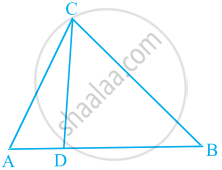
आकृति में, यदि ∠ACB = ∠CDA, AC = 8 cm और AD = 3 cm है, तो BD ज्ञात कीजिए।
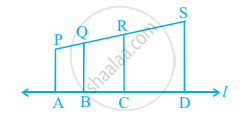
आकृति में, PA, QB, RC और SD में से प्रत्येक रेखा l पर लंब है, AB = 6 cm, BC = 9 cm, CD = 12 cm और SP = 36 cm है। PQ, QR और RS ज्ञात कीजिए।