Advertisements
Advertisements
Question
सड़क पर लगा एक बिजली का बल्ब एक खंभे पर सड़क के स्तर से 6 m ऊपर लगाया गया है। यदि 1.5 m लंबाई वाली एक महिला की छाया 3 m लंबी है, तो ज्ञात कीजिए कि वह महिला खंभे के आधार से कितनी दूरी पर खड़ी है।
Solution
मान लीजिए कि खंभे पर लगे स्ट्रीट बल्ब की स्थिति A है, AB = 6 m और CD = 1.5 m है, एक महिला की ऊंचाई है और उसकी छाया ED = 3 m है।
माना खंबे और महिला के बीच की दूरी x m है।
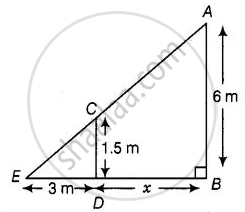
यहां महिला और खंभा दोनों लंबवत खड़े हैं।
तो, CD || AB
ΔCDE और ΔABE में,
∠E = ∠E ...[उभयनिष्ठ कोण]
∠ABE = ∠CDE ...[प्रत्येक 90° के बराबर]
∴ ΔCDE ∼ ΔABE ...[AAA समानता मानदंड द्वारा]
फिर, `("ED")/("EB") = ("CD")/("AB")`
⇒ `3/(3 + x) = 1.5/6`
⇒ 3 × 6 = 1.5(3 + x)
⇒ 18 = 1.5 × 3 + 1.5x
⇒ 1.5 = 18 – 4.5
∴ x = `(13.5)/1.5` = 9 m
अतः, वह खंभे के आधार से 9 m की दूरी पर है।
APPEARS IN
RELATED QUESTIONS
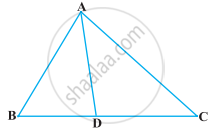
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
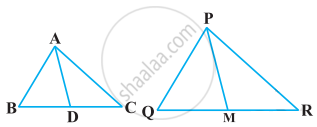
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है (देखिए आकृति)। दर्शाइए कि ∆ABC ∼ ∆PQR है।
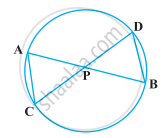
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠F = ∠C तथा AB = 3DE है। तब दोनों त्रिभुज ______ हैं।
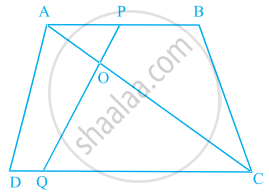
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
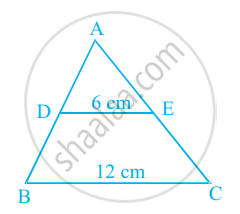
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
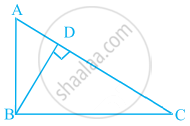
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।
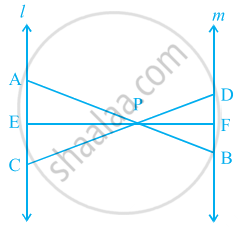
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।