Advertisements
Advertisements
Question
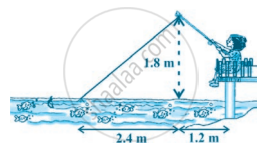
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए आकृति)? यदि वह डोरी को 5 cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाज़िमा की काँटे से क्षैतिज दूरी कितनी होगी?
Solution
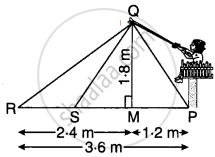
मान लीजिए कि नाजिया की प्रारम्भिक स्थिति P पर छड़ का सिरा Q पर, काँटे की स्थिति R पर तथा Q से PR पर डाले गये लम्ब के पाद की स्थिति M पर है। तब प्रश्नानुसार,
PR = 3.6, QM = 1.8 m एवं RM = 2.4 m
PM = PR – RM = 3.6 – 2.4 = 1.2 m
मान लीजिए कि डोरी की वर्तमान लम्बाई = l m तो समकोण
∆QMR में, ∠QMR समकोण है
QR2 = RM2 + QM2 [पाइथागोरस प्रमेय से]
l2 = (2.4)2 + (1.8)2
= 5.76 + 3.24
= 9.00
l = `sqrt9` = 3 m
5 cm/s की चाल से 12 s में डोरी की लम्बाई में कमी
= 12 × 5
= 60 cm
= 0.6 m
डोरी की नई लम्बाई QS = 3.00 – 0.60
= 2.40 m
अब समकोण ∆QMS में, ∠QMS समकोण है
(SM)2 = (QS)2 – (QM)2 [पाइथागोरस प्रमेय से]
(SM)2 = (2.4)2 – (1.8)2
= 5.76 – 3.24
= 2.52
SM = `sqrt2.52`
= 1.59 m
नाजिया की काँटे से नवीन दूरी = SP = SM + MP
= 1.59 + 1.2
= 2.79 m
अतः नाजिया की काँटे से अभीष्ट दूरी = 2.79 m है।
APPEARS IN
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
3 cm, 8 cm, 6 cm
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
13 cm, 12 cm, 5 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
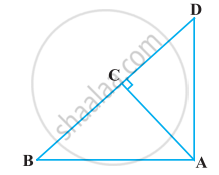
AD2 = BD.CD
ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB2 = 2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
18 m ऊंचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूँटे से जुड़ा हुआ है। खंभे के आधार से खूँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 m है।
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
भुजा 8 cm वाले एक समबाहु त्रिभुज का शीर्षलंब ज्ञात कीजिए।
10 m लंबी एक सीढ़ी, जो एक उर्ध्वाधर दीवार के सहारे टिकी हुई है, के निचले सिरे की दीवार के आधार से दूरी 6 m है। दीवार पर उस बिंदु की ऊँचाई ज्ञात कीजिए, जहाँ तक सीढ़ी का ऊपरी सिरा पहुँचता है।
18 m ऊँचे एक ध्वज स्तंभ की छाया की लंबाई 9.6 m है। इस स्तंभ के ऊपरी सिरे की छाया के दूरस्थ सिरे से दूरी ज्ञात कीजिए।
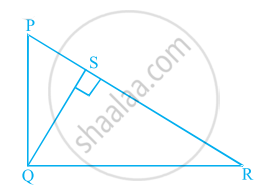
आकृति में PQR एक समकोण त्रिभुज है, जिसका ∠Q समकोण है तथा QS ⊥ PR है। यदि PQ = 6 cm और PS = 4 cm है, तो QS, RS और QR ज्ञात कीजिए।