Advertisements
Advertisements
प्रश्न
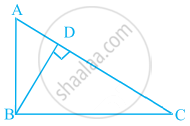
आकृति में, ABC एक त्रिभुज है जिसका ∠B समकोण है तथा BD ⊥ AC है। यदि AD = 4 cm, और CD = 5 cm है, तो BD और AB ज्ञात कीजिए।
उत्तर
दिया गया है, ΔABC जिसमें ∠B = 90° और BD ⊥ AC है।
साथ ही, AD = 4 cm और CD = 5 cm
ΔADB और ΔCDB में,
∠ADB = ∠CDB ...[प्रत्येक 90° के बराबर]
और ∠BAD = ∠DBC ...[प्रत्येक 90° – ∠C के बराबर]
∴ ΔDBA ∼ ΔDCB ...[AAA समानता मानदंड द्वारा]
फिर, `("DB")/("DA") = ("DC")/("DB")`
⇒ DB2 = DA × DC
⇒ DB2 = 4 × 5
⇒ DB = `2sqrt(5)` cm
समकोण ∆BDC में,
BC2 = BD2 + CD2 ...[पाइथागोरस प्रमेय द्वारा]
⇒ `"BC"^2 = (2sqrt(5))^2 + (5)^2`
= 20 + 25
= 45
⇒ BC = `sqrt(45) = 3sqrt(5)`
फिर से, ΔDBA ∼ ΔDCB,
∴ `("DB")/("DC") = ("BA")/("BC")`
⇒ `(2sqrt(5))/5 = ("BA")/(3sqrt(5))`
∴ BA = `(2sqrt(5) xx 3sqrt(5))/5` = 6 cm
अतः, BD = `2sqrt(5)` cm और AB = 6 cm।
APPEARS IN
संबंधित प्रश्न
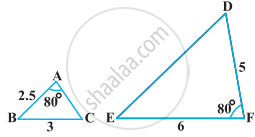
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
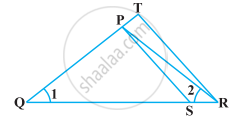
आकृति में, `"QR"/"QS"` = `"QT"/"PR"` तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔADB
AD और PM त्रिभुओं ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ∼ ∆PQR है। सिद्ध कीजिए कि `("AB")/("PQ") = ("AD")/("PM")` है।
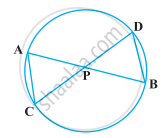
आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ∼ ∆DPB
(ii) AP.PB = CP.DP
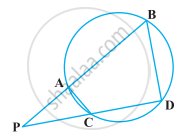
आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ∼ ∆PDB
(ii) PA.PB = PC.PD
दो समरूप त्रिभुजों की संगत भुजाएँ 2 : 3 के अनुपात में हैं। यदि छोटे त्रिभुज का क्षेत्रफल 48 cm2 है, तो बड़े त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
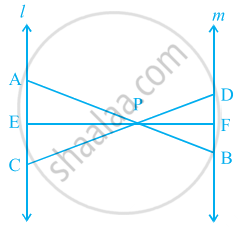
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।