Advertisements
Advertisements
प्रश्न
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ∼ ∆PQR है।
उत्तर
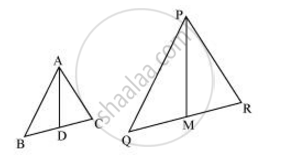
दिया गया,
`("AB")/("PQ") = ("AC")/("PR") = ("AD")/("PM")`
आइए AD और PM को क्रमशः बिंदु E और L तक इस प्रकार बढ़ाएँ कि AD = DE और PM = ML. फिर, B को E से, C को E से, Q को L से और R को L से मिलाएँ
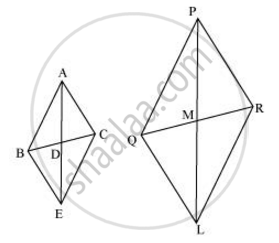
हम जानते हैं कि माध्यिकाएँ विपरीत भुजाओं को विभाजित करती हैं।
BD = DC और QM = MR
AD = DE ...(निर्माण द्वारा)
PM = ML ...(निर्माण द्वारा)
चतुर्भुज ABEC में, विकर्ण AE और BC एक दूसरे को बिंदु D पर समद्विभाजित करते हैं।
अत: चतुर्भुज ABEC एक समांतर चतुर्भुज है।
∴ AC = BE and AB = EC ...(समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं)
इसी प्रकार, हम सिद्ध कर सकते हैं कि चतुर्भुज PQLR एक समांतर चतुर्भुज है और PR = QL, PQ = LR
यह दिया गया है।
`=>("AB")/("PQ") = ("AC")/("PR") = ("AD")/("PM")`
`=>("AB")/("PQ")=("BE")/("QL")= (2"AD")/(2"PM")`
`=>("AB")/("PQ") = ("BE")/("QL") = ("AE")/("PL")`
∴ ΔABE ∼ ΔPQL ...(SSS समरूपता कसौटी)
हम जानते हैं कि समरूप त्रिभुजों के संगत कोण बराबर होते हैं।
∴ ∠BAE = ∠QPL ...(1)
इसी प्रकार, यह सिद्ध किया जा सकता है कि ΔAEC ∼ ΔPLR और
∠CAE = ∠RPL ...(2)
समीकरण (1) और (2) जोड़ने पर,
∠BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ ...(3)
ΔABC और ΔPQR में,
`("AB")/("PQ") = ("AC")/("PR")`
∠CAB = ∠RPQ
∴ ΔABC ∼ ΔPQR ...(SAS समरूपता की कसौटी)
APPEARS IN
संबंधित प्रश्न
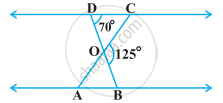
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° हैं। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।
ΔPQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ∼ ∆CFB है।
यदि दो त्रिभुजों ABC और PQR में, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)` है, तो ______।
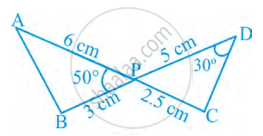
आकृति में, दो रेखाखंड AC और BD परस्पर बिंद P पर इस प्रकार प्रतिच्छेद करते हैं कि, PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° और ∠CDP = 30° है तब, ∠PBA बराबर ______ है।
यदि दो त्रिभुजों DEF और PQR मे, ∠D = ∠Q और ∠R = ∠E है, तो निम्नलिखित में से कौन सत्य नहीं है?
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
त्रिभुज PQR में, भुजा PR पर स्थित N एक ऐसा बिंदु है कि QN ⊥ PR है। यदि PN . NR = QN2 है, तो सिद्ध कीजिए कि ∠PQR = 90° है।
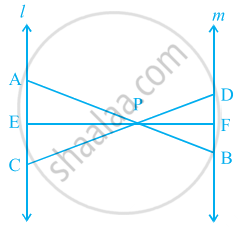
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।