Advertisements
Advertisements
प्रश्न
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
उत्तर
प्रश्न के अनुसार,
AB = 4 cm,
DE = 6 cm
EF = 9 cm
FD = 12 cm
भी,
∆ABC ∼ ∆DEF
हमारे पास है,
∴ `("AB")/("ED") = ("BC")/("EF") = ("AC")/("DF")`
⇒ `4/6 = ("BC")/9 = ("AC")/12`
पहले दो पद लेने पर, हमारे पास है,
⇒ `4/6 = ("BC")/9`
⇒ BC = `((4 xx 9))/6` = 6 cm
और अंतिम दो पदों को लेकर, हमारे पास है,
`("BC")/9 = ("AC")/12`
`6/9 = ("AC")/12`
AC = `(6 xx 12)/9` = 8 cm
अब,
∆ABC का परिमाप
= AB + BC + AC
= 4 + 6 + 8
= 18 cm
अत: त्रिभुज का परिमाप 18 सेमी है।
APPEARS IN
संबंधित प्रश्न
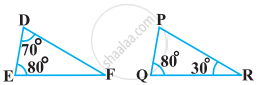
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
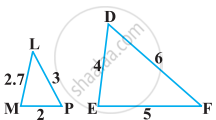
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔCDP
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔAEP ∼ ΔADB
CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ∼ ∆FEG है, तो दर्शाइए कि:
- `"CD"/"GH" = "AC"/"FG"`
- ∆DCB ∼ ∆HGE
- ∆DCA ∼ ∆HGF
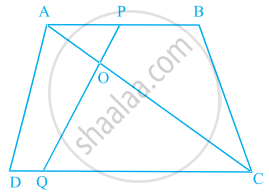
आकृति में, यदि AB || DC तथा AC और PQ परस्पर बिंदु O पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि OA. CQ = OC. AP है।
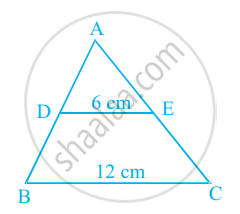
आकृति में, यदि DE || BC है, तो ar(ADE) और ar(DECB) का अनुपात ज्ञात कीजिए।
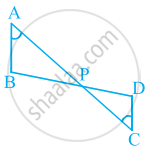
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
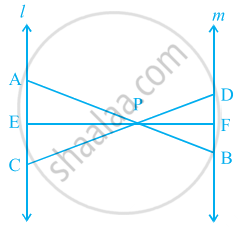
आकृति में l || m तथा रेखाखंड AB, CD और EF, बिंदु P पर संगामी हैं। सिद्ध कीजिए कि `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)` हैं।