Advertisements
Advertisements
प्रश्न
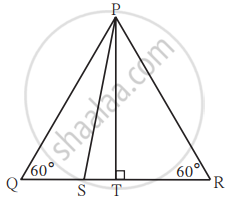
संलग्न आकृति में ΔPQR एक समबाहु त्रिभुज है जिसमें बिंदु S यह रेख QR पर इस प्रकार है कि, QS = `1/3`QR तो सिद्ध कीजिए कि; 9PS2 = 7PQ2
उत्तर
उपपत्ति : रेख PT ⊥ भुजा QR इस प्रकार खींचो कि, Q-T-R.
ΔPQR एक समबाहु त्रिभुज है |
∴ PQ = QR = PR .............(समबाहु त्रिभुज की भुजाएँ) .........(1)
∠Q = 60° .............(समबाहु त्रिभुज के कोण) .........(2)
ΔPQT में,
∠PTQ + ∠PQT + ∠QPT = 180° .............(त्रिभुज के सभी कोणों का योग 180°)
∴ 90° + 60° + ∠QPT = 180° ...........[रचना और (2) से]
∴ 150° + ∠QPT = 180°
∴ ∠QPT = 180° = 150°
∴ ∠QPT = 30°
∴ ΔPQT एक 30° - 60° - 90° त्रिभुज है |
∴ त्रिभुज के 30° - 60° - 90° के प्रमेय से,
PT = `sqrt3/2`PQ ............(60° की सम्मुख भुजा)
QT = `1/2`PQ ............(30° की सम्मुख भुजा)
QS + ST = QT ............(Q-S-T)
∴ `1/3`QR + ST = `1/2`PQ
∴ `1/3`PQ + ST = `1/2`PQ .............[(1) से]
∴ ST = `1/2`PQ - `1/3`PQ
∴ ST = `(3"PQ" - 2"PQ")/6`
∴ ST = `"PQ"/6`
ΔTPS में,
∠PTS = `90^circ` ...............(रचना)
∴ पायथागोरस के प्रमेय से,
`"PS"^2 = "PT"^2 + "ST"^2`
∴ `"PS"^2 = (sqrt3/2 "PQ")^2 + ("PQ"/6)^2`
∴ `"PS"^2 = (3"PQ"^2)/4 + ("PQ"^2)/36`
∴ `"PS"^2 = (27"PQ"^2 + "PQ"^2)/36`
∴ `"PS"^2 = (28"PQ"^2)/36`
∴ `"PS"^2 = (7"PQ"^2)/9`
∴ 9PS2 = 7PQ2
APPEARS IN
संबंधित प्रश्न
आकृति में ∠MNP = 90°, रेख NQ ⊥ रेख MP, MQ = 9, QP = 4, तो NQ का मान ज्ञात कीजिए।
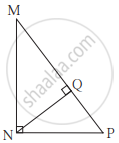
आकृति में ΔPSR में दी गई जानकारी के आधार पर RP और PS ज्ञात कीजिए।
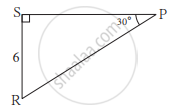
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
ΔABC में, यदि AB = `6sqrt3` सेमी, AC = 12 सेमी और BC = 6 सेमी हो, तो ∠A का माप कितना होगा?
किसी समबाहु त्रिभुज की भुजा 2a हो तो उसकी ऊँचाई ज्ञात कीजिए।
ΔRST में, ∠S = 90°, ∠T = 30°, RT = 12 सेमी हो तो RS तथा ST का मान ज्ञात कीजिए।
समबाहु ΔABC में आधार BC पर बिंदु P इस प्रकार है कि, PC = `1/3` BC, यदि AB = 6 सेमी तो AP ज्ञात कीजिए।
∆RST में, ∠S = 90°, ∠T = 30°, RT = 12 सेमी, तो RS का मान ज्ञात कीजिए।
