Advertisements
Advertisements
प्रश्न
सोचा गया कि x और y के निम्नलिखित मान एक रैखिक समीकरण को संतुष्ट करते हैं :
| x | 6 | – 6 |
| y | –2 | 6 |
वह रैखिक समीकरण लिखिए। उपरोक्त सारणी में दिए x और y के मानों का उपयोग करते हुए आलेख खींचिए। इस रैखिक समीकरण का आलेख निम्नलिखित को किस बिंदु पर काटता है?
- x-अक्ष
- y-अक्ष
उत्तर
दिया गया है, बिंदु (6, –2) और (–6, 6) हैं।
माना रैखिक समीकरण y = mx + c बिंदुओं (6, –2) और (–6, 6) से संतुष्ट होता है, फिर बिंदु (6, –2) पर
–2 = 6m + c ...(i)
और बिंदु (–6, 6) पर, 6 = –6m + c ...(ii)
समीकरण (i) में से समीकरण (ii) घटाने पर, हमें प्राप्त होता है।
12m = – 8
⇒ `m = (-8)/12`
⇒ `m = -2/3`
m का मान समीकरण (i) में रखने पर, हम पाते हैं।
`-2 = 6(-2/3) + c`
–2 = –4 + c
⇒ c = –2 + 4
⇒ c = 2
m = `- 2/3` और c = 2 को रैखिक समीकरण y = mx + c में रखने पर, हम पाते हैं।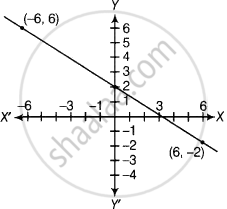
`y = -2/3x + 2`
⇒ `y = (-2x + 6)/3`
⇒ 3y = –2x + 6
⇒ 3y + 2x = 6
जब रैखिक समीकरण का ग्राफ
i. x-अक्ष को काटता है।
फिर, समीकरण 2x + 3y = 6 में y = 0 रखने पर, हमें प्राप्त होता है।
⇒ 2x + 3·0 = 6
⇒ 2x = 6
∴ x = 3
जब रैखिक समीकरण का ग्राफ
ii. y-अक्ष को काटता है।
फिर, समीकरण 2x + 3y = 6 में x = 0 रखने पर, हमें प्राप्त होता है।
⇒ 2·0 + 3y = 6
⇒ 3y = 6
∴ y = 2
इसलिए, रैखिक समीकरण का आलेख x-अक्ष को बिंदु (3, 0) पर और y-अक्ष को बिंदु (0, 2) पर काटता है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित समीकरण के चार हल लिखिए:
πx + y = 9
बताइए कि निम्नलिखित समीकरण x – 2y = 4 का हल है या नहीं:
(2, 0)
बताइए कि निम्नलिखित समीकरण x – 2y = 4 का हल है या नहीं:
`(sqrt2", "4sqrt2)`
बताइए कि निम्नलिखित समीकरण x – 2y = 4 का हल है या नहीं:
(1, 1)
रेखा y = x पर स्थित किसी बिंदु का रूप होता है
बिंदु (0, 3) रैखिक समीकरण 3x + 4y = 12 के आलेख पर स्थित है।
सारणी
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2 | 3 | 4 | –5 | 6 |
से प्राप्त बिंदुओं के निर्देशांक समीकरण x – y + 2 = 0 के कुछ हलों को निरूपित करते हैं।
उस सरल रेखा से निरूपित समीकरण का आलेख खींचिए जो x-अक्ष के समांतर है और उसके नीचे 3 मात्रक की दूरी पर है।
यदि एक द्रव का तापमान केल्विन मात्रकों में x°K है या फारेनहाइट मात्रकों में y°F है, तो तापमानों के मापन की दोनों पद्धतियों के बीच संबंध रैखिक समीकरण `y = 9/5 (x - 273) + 32` द्वारा दिया जाता हैं।
- यदि किसी द्रव का तापमान 313°K है, तो उसका फारेनहाइट में तापमान ज्ञात कीजिए।
- यदि तापमान 158°F है, तो केल्विन में तापमान ज्ञात कीजिए।
यदि एक द्रव का तापमान केल्विन मात्रकों में x°K है या फारेनहाइट मात्रकों में y°F है, तो तापमानों के मापन की दोनों पद्धतियों के बीच संबंध रैखिक समीकरण y = `9/5 (x-273) +32` द्वारा दिया जाता हैं।
यदि तापमान 158°F है, तो केल्विन में तापमान ज्ञात कीजिए ।
