Advertisements
Advertisements
प्रश्न
Solve the following quadratic equation for x:
`4sqrt3x^2+5x-2sqrt3=0`
उत्तर १
`4sqrt3x^2+5x-2sqrt3=0`
`rArr4sqrt3x^2+8x-3x-2sqrt3=0`
`rArr4x(sqrt3x+2)-sqrt3(sqrt3x+2)=0`
`rArr(4x-sqrt3)(sqrt3x+2)=0`
`therefore x=sqrt3/4` or `x=-2/sqrt3`
उत्तर २
`4sqrt3x^2+5x-2sqrt3=0`
`rArr4sqrt3x^2+8x-3x-2sqrt3=0`
`rArr4x(sqrt3x+2)-sqrt3(sqrt3x+2)=0`
`rArr(4x-sqrt3)(sqrt3x+2)=0`
`therefore x=sqrt3/4` or `x=-2/sqrt3`
APPEARS IN
संबंधित प्रश्न
Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x2 + x + 4 = 0
Find the roots of the quadratic equations 2x2 – 7x + 3 = 0 by applying the quadratic formula.
`x^2-(sqrt2+1)x+sqrt2=0`
The sum of the areas of two squares is `640m^2` . If the difference in their perimeter be 64m, find the sides of the two square
The area of a right triangle is `600cm^2` . If the base of the triangle exceeds the altitude by 10 cm, find the dimensions of the triangle.
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
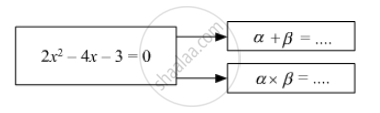
α, β are roots of y2 – 2y –7 = 0 find,
α2 + β2
The numerator of a fraction is 3 less than the denominator. If 2 is added to both the numerator and the denominator, then the sum of the new fraction and the original fraction is \[\frac{29}{20}\].Find the original fraction.
To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool?
The positive root of `sqrt(3"x"^2 + 6)` = 9 is:
